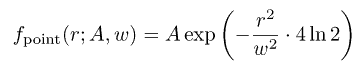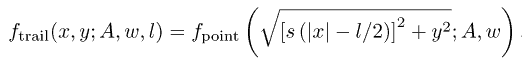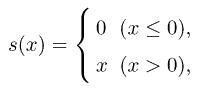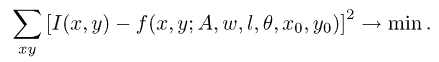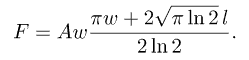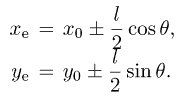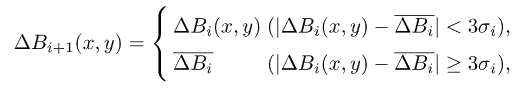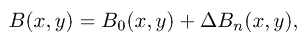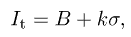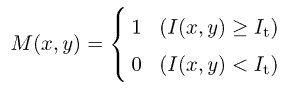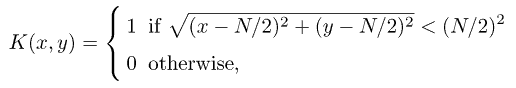Distinguishing Features of CCD Astrometry of Faint GEO Objects
Preprint submitted to Advances in Space Research
Central (Pulkovo) Observatory of the Russian Academy of Sciences,
196140, Pulkovskoye ave., 65/1, St. Petersburg, Russia
Abstract
The problem of initial reduction of CCD observations of faint GEO objects is studied. Several difficulties and questions arising in connection with image processing for this kind of observations are mentioned. A natural way to apply the PSF fitting technique to line-shaped trails of stars or GEO objects is described and illustrated by its implementation in the Apex II astronomical image processing package. Logical filtering technique to improve the automatic object detection is proposed. These rather convenient and versatile methods can increase astrometric and, to a lesser degree, photometric accuracy of faint GEO object observations.
1. Introduction
Currently, ground-based optical observations of geosynchronous Earth orbit (GEO) objects, including space debris, are mostly performed with small aperture telescopes, < 1.5 m in diameter. Despite having typically lower limiting magnitude and angular resolution, small aperture telescopes outperform large aperture ones in efficiency of observations of transient events, as well as in survey tasks, mostly due to their larger field of view. This is very important for the GEO monitoring problem.
The limited sensitivity of small telescopes in CCD observations of faint or fast moving objects is a significant challenge to observation and image processing techniques. Moreover, sooner or later larger telescopes meet exactly the same problem, when the need in observations of even fainter objects arises. In this paper we'll use the term "faint object" in the context of observations at the sensitivity limit, regardless of the particular telescope aperture or actual magnitude of the object. We assume that GEO (and close to GEO) objects require observations without sidereal tracking or with telescope locked on the target object to achieve maximum sensitivity. Both of these observation techniques lead to trailed field stars and/or target object. This tightly links the term "faint GEO object" to CCD images containing trailed sources.
CCD photometry of fast-moving objects is a demanding problem itself (see e.g. Krugly, 2004). In mid-nineties, Schildknecht and his colleagues studied the problem of CCD image processing in connection with observations of space debris in the GEO (Schildknecht et al., 1995). A number of questions and techniques related to processing of this kind of CCD images were also considered by Agapov et al. (2005). In this paper we'll mostly concentrate on the features of these images related to positional measurements.
Comparatively low astrometric accuracy of individual observations remains one of the most important sources of the orbital data uncertainty for GEO objects. To achieve the good quality of individual coordinate measurements, the usual image processing tasks (including calibration, filtering, and object extraction) should be followed by two specific steps which comprise the astrometric reduction itself. First, accurate positions of reference stars are required to obtain the differential astrometry solution. Second, the target object position (which has to be precisely determined as well) needs to be reduced into the same reference frame to compute the final celestial coordinates of the target object for the given epoch.
Unfortunately, a number of factors contribute to the lower accuracy of reference star positions within a single CCD frame: atmospheric turbulence, mechanical instability of the telescope, finite mechanical CCD shutter speed, defects of the telescope optics, and low signal-to-noise ratio (SNR) of faint stars. Atmospheric turbulence distorts the shapes of star trails within the image plane and produces peaks and cavities; unlike CCD images acquired with sidereal tracking, these effects are not being averaged over the whole exposure time, leading to the Gaussian or similar profile. Moreover, atmospheric distortions differ across the whole frame, making it difficult to account for unambiguously. Vibration of the telescope tube acts in the similar way, although its effect is at least the same across the whole field of view. Finite velocity and instability of the CCD shutter leads to uncertainty of positions of the star trail endpoints; thus for this kind of observations frame transfer CCDs seem to be preferred over the more widespread full-frame CCDs. Optical aberrations, which are'characteristic mostly of large field of view instruments, distort trail shapes in a complex manner and lower their SNR. Finally, comparatively low SNR and the lack of bright reference stars, typical of observations with small aperture telescopes without sidereal tracking, also contribute to large position errors of reference stars.
These problems altogether increase the final astrometric error in faint GEO object observations to several times the error achievable for untrailed sources with the same telescope. One should mention that some of these issues can be partially reduced by a better telescope design, but they cannot be completely eliminated, while others are unavoidable by nature.
From the image processing point of view, three basic methods to determine trail positions in pixel coordinates exist:
- barycenter positions;
- PSF fitting;
- edge detection.
Being the easiest and the most computationally effective one, the barycenter technique is obviously the most inaccurate of these three. Barycenter positions of trails are heavily distorted by atmospheric turbulence, especially by extinction fluctuations, which can shift measured positions by several pixels, compared with point source images, where barycenter positions are at least accurate down to a single pixel. Rapid time variability of the object's brightness, which is a common feature of most GEO objects, also contributes to large error of the barycenter position.
Techniques based on the edge detection - usually by gradient filtering - are much more accurate; however they tend to fail at low SNRs - also due to brightness variations along the trail.
The widely used point spread function (PSF) fitting technique seems to be the most robust and versatile way to obtain the accurate trail positions. It has proven to produce reasonable results even for star trails of extremely low SNR (< 1 for the entire trail) and those heavily distorted by atmospheric turbulence; it is relatively easy to customize for a wide range of telescope parameters and observation conditions. The present paper focuses on the application of the PSF fitting technique to CCD images containing trailed sources and on the implementation of this technique in Apex II, a software platform for astronomical image processing, developed at Pulkovo observatory.
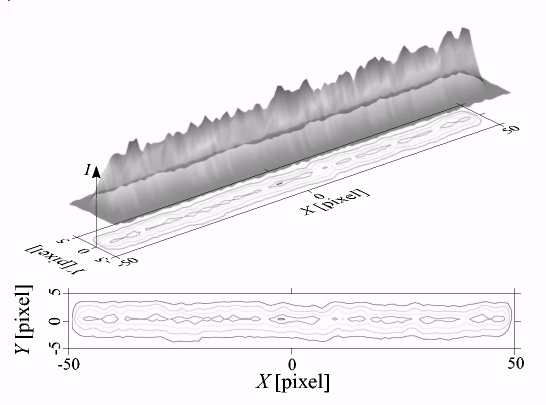
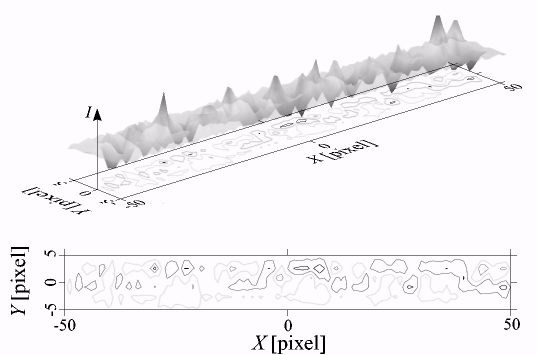
Fig. 1. Typical star trail image: (a) 512 X 512 CCD frame with star trails (sample star and target space debris object are indicated by arrows); (b) intensity distribution along the star trail: 3D image and contour plot
2. PSF fitting in case of trailed sources
When working with real CCD images containing trailed sources, one has to deal with trails distorted by atmospheric turbulence. Fig. 1 shows a typical case of a high-SNR star in a moderately crowded field. (The image has been obtained on the Zeiss-600 D = 600 mm f/12 Cassegrain telescope, 12x12-arcmin field of view with 1K X 1K Kodak sensor, at Maidanak observatory, one of those participating in the PulCOO collaboration (Molotov et al., 2005; Agapov et al., 2006))
The basic idea of the PSF fitting procedure in this case is to use a model profile of a trail extended along the direction inferred by either the apparent diurnal motion (for stars) or the apparent velocity of the object (for GEO and other high-orbit objects). One starts from a symmetric Gauss/Lorentz/Moffat or some other point source profile fpoint (r; A, w), where r is the radial distance in pixels, A is the peak intensity of the trail, and w is the expected full width at half maximum (FWHM) of a point source, in pixels, determined by the observed seeing. For instance, in case of the Gaussian PSF, fpoint reads as
Let us assume that the X axis is directed along the trail, while the Y axis goes across the trail in the "local" reference frame associated with the PSF. The symmetric PSF fpoint is then stretched in the X direction, assuming constant intensity along the whole trail for any given y. The resulting PSF for trails (Fig. 2) is defined by
Fig. 2. Model line-shaped PSF
where
and l is the expected trail length.
Trail orientation in the "global" image reference frame is defined by the angle θ. Finally, if (x0, у0) is the position of the trail centroid in image coordinates, the expression takes the form
Trail PSF in this form is directly fit to the actual intensity data I(x, у) in the immediate vicinity of the trail:
Nonlinear least-squares fit (e.g. using the Levenberg - Marquardt algorithm (More, 1977)) gives the estimates of the trail shape parameters (A, w, l) and its precise location within the image (x0, y0). Flux from a star or a GEO object can be easily derived from the trail shape parameters, which virtually eliminates the need in aperture photometry in applications without strict requirements on the photometric accuracy. For instance, in case of the Gaussian PSF, flux is given by
Fig. 3 demonstrates residual intensity after PSF fitting for the real star trail shown in Fig. Ib.
Fig. 3. Intensity residuals after PSF fitting
This procedure is applied independently to any trailed object within the image, individual trail orientation and length (θ and l) for the particular object being nothing else than two of several other varying parameters in the least-squares adjustment.
When appropriate, this technique could be easily extended to the case of time-varying intensity or even to accommodate a transverse jitter of the photocenter to further adapt the model PSF to the real one. Although, it seems to be more natural to achieve the same result by extracting the real PSF from a set of stars, than by inventing some complex analytical expression.
Depending on the capabilities of the imaging and timing system of the telescope, better astrometry results could be achieved by relying upon the trail endpoints rather than its centroid (x0, у0) - PSF fitting then produces endpoint positions (xе, ye) straightforwardly:
The presented PSF fitting technique has proven to be very stable with respect to both intensity fluctuations along the trail and jitter in the transverse direction, which significantly reduce positional accuracy of the two other methods mentioned above, or even render measurement impossible. As shown by Biryukov, Rumyantsev (2002), in many practical applications PSF fitting gives the most accurate estimates of the trail parameters possible.
3. Overview of the Apex II image processing package
We have implemented the PSF fitting algorithm described in Section 2 in the Apex II package for astronomical data reduction. This package is currently being developed at Pulkovo Observatory and used throughout the whole PulCOO collaboration (Molotov et al., 2005; Agapov et al., 2006) for initial reduction of raw observations of various near and deep space objects. This section briefly describes basic features and design concepts of the package.
Apex II is a general-purpose software platform for astronomical image processing. Its architecture and design principles are similar to those of the major image processing packages including IRAF, MIDAS, and IDL. Much like them, Apex II consists of several key components:
- core with embedded high-level interpreted dynamic
(scripting) programming language;
- standard library of general-purpose utility functions and
specific astronomical image processing algorithms;
- object-oriented graphical user interface (GUI) subsys
tem for interactive image examination and data plotting,
built on top of the core language and library;
- a set of user functions and scripts which utilize the above
components to solve the particular image processing
problems.
This structure has proven to be most flexible and versatile. It allows to implement the full range of image processing applications - from conventional command-line driven tools with interactive examination of intermediate processing results to fully automated pipelines for the processing of large data volumes, and stand-alone GUI applications for specific image reduction tasks.
Unlike the image processing packages mentioned above, Apex II is not based upon a dedicated interpreted programming language, but rather upon the widely used general-purpose object-oriented scripting language Python (
http://www.python.org). This choice is motivated primarily by the clarity, power, and flexibility of the language, existence of implementations for all major hardware and software platforms, and the extensive standard library for most routine tasks like input/output, data visualization, matrix algebra, curve and surface fitting, n-dimensional image processing etc. Despite the widespread opinion about the low performance of scripting languages, pure Python scripts in Apex II are often faster than similar programs written in conventional compiled programming languages. This is mostly due to the high level of vectorization of mathematical operations and to effective optimization of underlying C/Fortran libraries.
The standard Apex II library is built primarily on top of the two Python packages, Numerical Python and Scientific Python (NumPy/SciPy,
http://www.scipy.org). The first of them implements the basic functionality for working with multidimensional arrays, including vectorization and matrix algebra. The second one provides implementation of most of the algorithms commonly used in scientific applications: Fourier transform, integration, solving PDEs, interpolation, optimization and nonlinear least-squares fitting, signal and image processing, special functions etc. Based on these algorithms, as well as on the built-in Python functions, the Apex II library implements various higher level tasks specific to the field of astronomical image processing, like timescale conversions, calibration and filtering of CCD images, automatic object detection, PSF fitting, astromet-ric and photometric reduction, access to star and other catalogs, including ephemeris systems, and so forth.
The graphical subsystem (still under active development) is based on wxPython (
http://www.wxpython.org), the cross-platform GUI toolkit, and on matplotlib (
http://matplotlib.sourceforge.net), the scientific data visualization package for Python. These packages can be used to display individual CCD frames or catalog fields, plot various data obtained during image processing, as well as create standalone GUI applications intended for processing of specific kinds of astronomical images.
Thus, Apex II is primarily a general-purpose software platform for the development of reduction systems for various astronomical data. Modules related to some specific task (like minor planet astrometry or GEO object image processing) are organized in separate packages.
The following section illustrates the main pipeline for processing of GEO object observations in Apex II. Also, some peculiarities of this kind of astronomical images are highlighted.
4. Apex II Image processing pipeline for GEO objects
The standard automatic reduction process for GEO object observations includes the following basic steps:
- loading an image (usually stored as a FITS file);
- standard bias/dark/flat calibration and defect correction (optional);
- sky background flattening (optional);
- image filtering and enhancement to increase SNR (optional);
- global thresholding;
- logical filtering to eliminate noise and reduce trail fragmentation (optional);
- segmentation;
- deblending (optional);
- isophotal analysis;
- PSF fitting;
- final rejection of spurious detections;
- reference astrometric catalog matching;
- differential astrometry;
- differential photometry;
- report generation.
The first steps of the pipeline, related to object extraction, are similar to the classical approach of SExtractor (Bertin, Arnouts, 1996). Most of the terms and algorithms involved in object detection are described in this paper. However, specific features of space debris observations - e. g. clear distinction between stars and GEO objects and the predetermined star trail orientation - allow for a number of optimizations which reduce the processing time and the number of false detections. Separate steps of the pipeline, with particular focus on these optimizations and peculiarities of this type of CCD images, are discussed below.
Fig. 4. Sky background estimation: (a) original image; (b) estimated background map; (c) image after background subtraction: median filter; (d) image after background subtraction: smoothing + sigma clipping. All images are 512 x 512 pixels
4.1. Input image
The sample raw image shown in Fig. 4a (same field as in Fig. la) represents the rather uncommon situation of many bright reference stars (field in the Milky Way). Probably, a shorter exposure time should be chosen here to reduce overlapping of star trails.
4.2. Image calibration
This step includes the conventional bias/dark/flat correction and elimination of column defects. Indeed, unless precise photometry is required, this step can be ultimately skipped as it appears to have no effect on the resulting astrometric accuracy. Only severe column defects should be removed, while substantial background inhomogeneities can be easily handled at the next step.
In the general case, dead and hot pixels might be also eliminated at this stage. Although, sparse dead pixels generally have negligible effect on the resulting astrometric accuracy, while hot pixels, emerging later as occasional spurious detections, are removed at the subsequent filtering and rejection stages (see Sections 4.6 and 4.10 below).
The only situation when the standard calibration sequence can help is the case of very faint GEO objects accompanied by strong background inhomogeneity, often due to vignetting. As it will be shown below in Section 4.3, on-the-fly background estimation can prevent automatic detection of low-SNR objects in this case. Moreover, PSF fitting may produce erroneous results for such objects, when background variation along the object is of the same order as the object's own intensity.
4.3. Sky background estimation and subtraction
Background flattening is critical for automatic object detection using the global thresholding technique if the image background is highly non-uniform (see Fig. 4b), which is usually due to vignetting, light pollution, Moon, thin clouds etc. In Apex II, the image background map can be estimated using the following two algorithms:
- median filtering with large kernel (about 0.2-0.25 of
the image size);
- smoothing of an undersized image with subsequent sigma clipping.
Median filter (Fig. 4c) acts in a straightforward way, extracting large-scale details of the image. Among its advantages is the ability to preserve faint objects and noise characteristics of the original image. Unfortunately, the kernel size cannot be set very small, as this kills objects - especially star trails - within the image. Thus the algorithm cannot deal with small-scale background variations and is also comparatively slow.
The second sky background estimation method (Fig. 4d) first shrinks the original image I(x, y) down to about 0.1 of its initial size, using spline filter to minimize aliasing artifacts; this small image is then smoothed by a median filter (with a much smaller kernel than in the first algorithm), enlarged to the original size and slightly blurred by a Gaussian filter. The resulting map B0(x,y) is then used as the initial guess in the iterative sigma clipping process
where ΔBi and σi are the mean and standard deviation, respectively, of the background map correction ΔВi(x,у) at i-th iteration, and ΔB0(x, y) = I(x, y) - B0(x, y). The final background map is computed as
where n is the number of iterations.
Unlike the first algorithm, this one is comparatively fast and can eliminate also small-scale sky background variations. The obvious side effect of the latter feature is that this method kills objects with very low SNR. Also, upon subtraction, it introduces additional noise coming from the original image; however, this can be partially avoided by reasonably smoothing ΔBn(x, y).
One should note that both algorithms are able to estimate the sky background map even from a single CCD frame; thus no calibration frames or any other external data are required, which simplifies the observation procedure.
Fig. 5. Bit mask and logical filtering: (a) bit mask after thresholding; (b) effect of symmetric logical filter; (c) effect of asymmetric logical filter with kernel stretched in the direction of diurnal motion of stars. All images are 512 x 512 pixels
4.4. Image filtering and enhancement
Unfortunately, most of conventional PSF-based image enhancement and restoration techniques are not suitable for images with star/GEO object trails, since they strongly rely on the assumption of knowledge of the exact PSF shape, while the actual shapes of trailed objects are usually very far from the "ideal" ones due to atmospheric turbulence.
The only promising method seems to be shift-combining a series of individual frames to increase SNR of either reference stars or the target object (see e.g. Yanagisawa et al., 2002). This method, however, being very computationally expensive, also reduces the temporal accuracy of measurements which is critical for orbit determination; thus, it is more applicable to surveys and search of new space debris objects than to precise astrometry and orbit improvement.
4.5. Thresholding
For a filtered image with flat background, the global detection threshold level is computed as
where В is the global background level computed as either the sigma-clipped mean or the modal intensity across the whole image, σ is the noise level, and k is the manually set threshold factor. Also, for better automatic threshold estimation, Apex II can fit a noise model to the image histogram, which may produce more accurate values of В and σ if the actual noise distribution function is close to the noise model chosen. Due to the frequent lack of bright reference stars (at least 3 or 4 stars are required for astrometry) , and with focus on automatic detection of faint GEO objects, the threshold factor k for this kind of observations is usually set as low as 2.5-3.
Thresholding produces a bit mask (an image of 0's and 1's)
(Fig. 5a). One can see many faint stars split into separate unconnected chains of pixels, as well as the numerous overlapping star trails.
4.6. Bit mask (logical) filtering
Immediately after thresholding, due to the low detection level (see Section 4.5), the bit mask, even for a previously filtered image, is crowded with a vast number of noise streaks. To reduce the probability of false detections and, on the other hand, to improve detectability of faint objects with low SNRs, Apex II performs logical filtering of the bit mask. It is somewhat similar to conventional filtering of a grayscale image, though appears to be more robust and less noisy.
The idea behind the logical filter used is rather simple. A square-shaped filter kernel is defined as
where N is the filter kernel size chosen in such a way that the kernel fully covers a point source. In other words, the kernel contains 1's inside the circle of the same size as an average point source within the image, and 0's outside this circle. After the kernel is applied to the whole bit mask, pixels with values above some threshold are set to 1, while others are set to 0. For each image pixel, the filter effectively counts the number of neighbor pixels that lie above the detection threshold. Isolated pixels which have no or few neighbors in their immediate vicinity of the characteristic size of a point source are thus wiped out. On the contrary, pixels tending to group into clusters are retained, even if they were not present in the unfiltered bit mask due to the original intensity lying below the detection threshold It.
Two variants of this logical filter are used in Apex II for processing of GEO obejct observations. The first one acts exactly as described above. It has the same effect on the target object and on the reference star trails and thus may be used in most circumstances.
Unfortunately, the lack of bright field stars is not an uncommon situation in GEO object observations with small aperture telescopes. Faint stars with low SNR, on the other hand, are often "broken" into several pieces by noise and intensity fluctuations (see Section 2), which prevents their detection and measurement or at least distorts their positions and lengths. The original symmetric logical filter cannot paste these fragments together. For this purpose, one more filter is introduced, which is a natural extension of the original symmetric filter to the case of trails. The circular region of 1's in the filter kernel (see above) is simply stretched in the expected direction of the star trails. This virtually eliminates star trail fragmentation. However, the filter affects also the target GEO object, which generally moves in the different direction than the stars; the target object may thus disappear after this sort of filtering. Hence we can conclude that the asymmetric logical filter is most suitable in circumstances of a bright slow target GEO object and lack of bright field stars. Figs. 5b,c demonstrate the effect of these two filters on the bit mask.
The logical filtering technique has proven to effectively clear the bit mask from the numerous dots scattered across the image, which are unavoidable for such low threshold factors k. At the same time, it may significantly increase the number of detected reference stars, which is important for accurate astrometry. We should point out that this kind of filtering does not directly increase the SNR of trailed sources; instead, it reduces the probability of faint star trail fragmentation. Therefore, it is rather hard to exactly estimate the faint limit improvement achieved with logical filtering, since it depends on many atmospheric and instrumental conditions; generally, the worse are these conditions, the better is the benefit from filtering. For instance, regarding the telescopes participating in PulCOO, in most practical situations the faint limit increases by 1-2 magnitudes when the logical filter is applied.
Moreover, the same asymmetric logical filter, with 1's in the kernel replaced by 0's and vice versa, can efficiently perform the opposite task of elimination of star trails for the purpose of automatic GEO object detection.
4.7. Segmentation
Segmentation (i.e. identification of individual objects above the detection threshold) in Apex II involves the connectivity properties of pixel groups. Experiments have shown that the most reliable method is based upon the detection of 4-connected groups of pixels. An alternative implementation is based on the Lee path connection method (Lee, 1961) widely used in electric engineering for routing printed circuit boards.
4.8. Deblending
Crowded fields and incorrect choice of exposure duration frequently result in overlapping (blending) of multiple field stars with each other or with the target GEO object. Conventional deblending (see Bertin, Arnouts, 1996) utilizes the "multithresholding" technique, where a composite object is being split into separate connected groups of pixels at a number of levels spanning the intensity range from the initial detection threshold It (see Section 4.5) to the peak intensity. This approach is usually of little help for trailed sources, since the trails are split back into separate fragments, which renders the multithresholding technique not only useless, but dangerous. An adequate deblending algorithm for the case of line-shaped object images is still a major problem.
4.9. Isophotal analysis
This step produces initial guess for the whole set of trail parameters - centroid position x0 and y0 (see Section 2), length l, width w, orientation θ, and amplitude A. Preliminary rejection of spurious detections is also performed here - groups of pixels that are either too narrow or too wide to be the real objects are excluded from processing.
Fig. 6. PSF fitting and rejection: (a) model profiles of both point sources and trails produced by PSF fitting; (b) residual image; (c) reference stars left after rejection of spurious detections. All images are 512 x 512 pixels
4.10. PSF fitting
PSF fitting for the case of line-shaped objects was described in detail in Section 2. Based on the isophotal analysis results, Apex II automatically switches to the "trail fitting" mode when appropriate; for point sources, the conventional PSF fitting using one of the standard PSF shapes (asymmetric Gaussian etc.) is performed.
The quality of implementation of the PSF fitting step is crucial to the overall accuracy of the target object coordinates. Among many other possible issues that may arise during PSF fitting, we can mention the following two:
- PSF fitter may fail for heavily overlapping trails;
- objects with very low SNRs or surrounded by rapidly
changing background may produce some strangely-
looking artifacts.
One should note that the PSF fitting stage in Apex II is performed on the input image with no sky background subtracted. The latter is quite an ambiguous and not well-defined entity; incorrect estimation of sky background might cause systematic errors in both photometry and astrometry. For this reason, the background map is used only at the object detection stage, to make it possible to apply a single threshold to the whole image. To account for the background level and its possible rapid variations, the PSF fitter in Apex II adds an optional constant or linear substrate to the model PSF.
Figs. 6a,b show a plot of the model object profiles produced by PSF fitting and the corresponding residual frame (input image minus model profiles), respectively. Ideally, Fig. 6b should not differ from the sky background map shown in Fig. 4b, at least to within the noise. Instead, one can see that the fitter failed for two kinds of objects: overlapping star trails and several very faint stars (actually, with SNR below 1).
Experiments have shown that the intrinsic accuracy of the PSF fitting technique applied to trailed sources is about a few hundredths of a pixel for objects with high SNR (> 20), and sometimes goes down to 0.01 pixel. Accuracy for faint sources is generally lower; nevertheless, even for objects with SNR below 3, it rarely exceeds 0.1-0.3 pixel.
4.11. Rejection of false detections
Because of the comparatively low detection level (see Section 4.5), and even after the logical filtering (Section 4.6), the image is usually contaminated by numerous artifacts coming from noise streaks, fragments of faint star trails etc.; cosmic rays should be rejected as well. Luckily, a priori knowledge of the expected shape parameters of real objects - first of all, of their width (seeing) and length and orientation of star trails - allows one to efficiently rule out spurious detections. For instance, even in the case of an un-dersampled image with seeing approximately equal to one pixel, FWHM of a Gaussian for artifacts with sharp edges (like cosmic rays) appears to be about 0.2-0.5 pixels, which makes it easy to distinguish them from the real objects.
In Apex II, a series of rejection criteria is applied to all detections sequentially. Apart from the FWHM constraints mentioned above, these include: upper limit for SNR, reasonable centroid position (within the image boundaries and not very far from the one produced by isophotal analysis), and length and orientation of the star trail. As a result of this step, only reference stars of good quality are left (Fig. 6c), which is critical to the subsequent reference catalog matching and astrometric reduction (see Sections 4.12,4.13 below).
4.12. Reference catalog matching
Apex II exploits a number of cross-identification algorithms. The three major ones are:
- an improved version of the translation-invariant "distance-orientation" algorithm (Kosik, unpublished);
- translation/rotation/flip/scale-invariant triangle pattern matching algorithm by Valdes et al. (1995);
- translation/rotation/flip-invariant version of the algorithm by Valdes et al. (1995); though being sensitive to the image scale, it is less prone to false identifications than the previous one.
All algorithms listed above involve only positional information. According to our experience, flux data are helpful only to exclude objects of deliberately different brightness from identification; using them as one of the matching criteria might lead to strong ambiguities.
4.13. Differential astrometry
During this stage, Apex II obtains the least-squares plate constants (LSPC) solution with outlier rejection in the framework of some reference astrometric catalog. Depending on the field of view and limiting magnitude, various catalogs can be used. Currently, Apex II supports HIPPAR-COS, Tycho-2, UCAC2, USNO-A, and USNO-B.
To achieve the best results, the appropriate plate model should be applied. Among others supplied by Apex II, the most useful ones are:
- 6 constant model
(here (x, у) here are the "measured" object coordinates obtained from the image, while (x', у') are their "predicted" coordinates deduced from catalog positions);
- 8 constant model
- 6 constant model with radial and tangential (decentric) distortion (Brown, 1966)
Of these three, the 8 constant model can account for non-zero tilt of the CCD sensor's normal to the optical axis and, partially, for differential refraction. The latter model may be useful for wide-field surveys and generally in circumstances when residual aberrations are not negligible.
4.14. Photometric catalog matching and reduction
This step is completely identical to that for untrailed sources. Either aperture or PSF fluxes can be utilized to estimate the target object magnitude. In most cases, both approaches give identical results. However, PSF fluxes are more accurate in case of a heavily crowded fields and for faint objects. Surprisingly, they produce more precise results also for undersampled images, when a point source occupies nearly a single pixel; this could probably be explained by the fact that aperture flux in this case is more affected by noise fluctuations of each individual pixel. Thus it seems natural to use fluxes provided by PSF fitting to estimate the GEO obejct magnitudes - especially as they might be regarded as a by-product of astrometric reduction.
To obtain the photometry solution, Apex II reduces the magnitudes of reference stars into the instrumental system. Measured magnitudes are then fit to catalog ones using either a linear or a polynomial model which gives the desired GEO object brightness estimation.
4.15. Report generation
This is the last stage of the automatic reduction process for GEO object observations. All GEO objects that were detected and measured are written to the final report file in the particular format according to the user's preference.
There are actually several versions of the pipeline presented above. Each of them is suited to some kind of GEO object observations and exploits the specific features of these observations to achieve the maximum accuracy, reliability, and computation speed. For example, there are separate versions of the pipeline for faint space debris follow-up sessions and for wide-field GEO region surveys. Each of them is intensively parameterized and can accommodate a variety of properties of the particular telescopes.
Finally, the main pipeline is accompanied by a number of pre- and post-processing scripts intended to convert the CCD frames to the proper format and to estimate the final accuracy of observations.
Conclusions
In this paper, we have considered a number of difficulties and questions that arise in the problem of initial reduction of CCD observations of GEO objects at the sensitivity limit. A simple technique applying the widely used PSF fitting method to CCD images containing line-shaped trails of stars or GEO objects was described. This technique improves astrometric and, to a lesser degree, photometric accuracy of GEO object observations. This technique is rather general and versatile and can be adapted to various peculiarities of instrumentation and observation program types, from faint space debris follow-up sessions to wide-field surveys. The trail PSF fitting technique itself, of course, does not provide the capability to detect faint objects, but is ensures the maximum accuracy and reliability of their measurement.
Currently, intrinsic positional accuracy of the best individual GEO object observations reaches 0.01 pixel, which is quite common in the world of point-like images. However, results of such quality can be achieved, first of all, in perfect atmospheric conditions; 20-30 times lower accuracy is far more frequent, especially for faint objects. Further development of the PSF fitting technique is one of the possible ways to raise the astrometric accuracy of GEO object observations to a new level.
The method presented, along with other image processing techniques, is implemented within the framework of Apex II, a general-purpose software platform for astronomical data reduction being developed at Pulkovo observatory. Since 2005, various applications built on top of the Apex II package are working at the observatories participating in the PulCOO collaboration. Some typical tasks solved by the package include: image calibration and examination, ephemeris interpolation, and, first of all, automated reduction of large series of images - starting from the raw images and ending with time series of the GEO objects' coordinates and magnitudes.
We briefly describe the basic design concepts of Apex II and its application to the automated GEO object image processing task. The logical filtering technique is proposed, which can increase the reliability and sensitivity of object detection.
Although the package is successfully used on a routine basis, there are still many things to enhance and improve. Among them, the most important are: image restoration and combining techniques to increase sensitivity and accuracy for faint objects; deblending of overlapping star trails; atmospheric jitter compensation for better accuracy with bad seeing conditions; integrated support for orbit determination, identification of GEO objects, and computation of ephemerides. These are the primary goals for future development.
Acknowledgements
The author is pleased to thank COSPAR for financial support of his attending the COSPAR'2006 meeting, and to Igor Molotov for encouragement of research presented here.
References
- Agapov, V., Biryukov, V., Kiladze, R., Molotov, I., Rumyantsev, V., Sochilina, A., Titenko, V. Faint GEO Objects Search And Orbital Analysis. Proceedings of the 4th European Conference on Space Debris, 18-20 April 2005, Darmstadt, Germany. ESA Publication SP-587, 153-158, August 2005.
- Agapov, V., Schildknecht, Т., Akim, E., Molotov, I., Titenko, V., Yurasov, V. Results of GEO space debris studies in 2004-2005. 57th IAC Final Papers DVD, Valencia, Spain, October 2-6, 2006, 15 pages, IAC-06-B6.1.12.
- Bertin, E., Arnouts, S. SExtractor: software for source extraction. Astron. Astrophys. Suppl. Ser., 117, 393-404, 1996.
- Biryukov, V., Rumyantsev, V. Limited accuracy of asteroid trails estimation at observations with CCD detectors, in: Barbara Warmbein (Ed.), Proceeding of Asteroids, Comets, Meteors - ACM 2002, ESA SP-500. Nordwijk, Netherlands: ESA Publications Division, 405-408, 2002.
- Brown, D. C. Decentric distortion of lenses. Journal of Pho-togrammetric Engineering and Remote Sensing, 32(3), 444-462, 1966.
- Kosik, J. Cl. Star pattern identification: Application to the precise attitude determination of the Auroral Spacecraft. Presentation given at the Space Research Institute of the Russian Academy of Sciences, available at http://www.iki.rssi.ru/seminar/virtual/kosik.doc.
- Krugly, Yu. N. Problems of CCD photometry of fast-moving asteroids. Sol. Sys. Res. 38(3), 241-248, 2004.
Lee, C. Y. An Algorithm for Path Connections and its Applications. IRE Trans. Electronic Comput., EC-10, 2, 346-365, 1961.
- Molotov, I., Agapov, V., Titenko, V., Khutorovsky, Z., Burtsev, Yu., Guseva, I., Rumyantsev, V., Ibrahimov, M., Kornienko, G., Erofeeva, F., Biryukov, V., Vlasjuk, V., Kiladze, R., Zalles, R., Sukhov, P., Inasaridze, R., Ab-dullaeva, G., Rychalsky, V., Kouprianov, V., Rusakov, O., Korotkiy, S., Filippov, E. International scientific optical network for space debris research. Submitted to Adv. Space Res.
- More, J. J. The Levenberg-Marquardt algorithm: implementation and theory, in: Watson, G. A. (Ed.), Numerical Analysis, Lecture Notes in Mathematics 630, Springer-Verlag, Heidelberg, 105-116, 1977.
- Schildknecht, Т., Hugentobler, U., Verdun, A. Algorithms for ground based optical detection of space debris. Adv. Space Res., 16(11), 47-50, 1995.
- Valdes, F. G., Campusano, L. E., Velasquez, J. D., Stetson, P. B. FOCAS automatic catalog matching algorithms. PASP, 107, 1119-1128, 1995.
- Yanagisawa, Т., Nakajima, A., Kimura, Т., Isobe, Т., Fu-tami, H., Suzuki, M. Detection of Small GEO Debris by use of the stacking method. Trans. Jpn. Soc. Aero. Space Sci., 44, 190-199, 2002.
Размещен 18 апреля 2007.