Ãëàâíàÿ Íîâîñòè ÏóëÊÎÍ ÐÑÄÁ Îáñåðâàòîðèè Ïóáëèêàöèè About us Êîíòàêò
Russian Academy of Sciences
Central Astronomical Observatory at Pulkovo

SIXTH US/RUSSIAN
SPACE SURVEILLANCE WORKSHOP

August 22-26, 2005

Proceedings
Edited by P. Kenneth Seidelmann and Victor K. Abalakin

St. Petersburg, 2005

APPLICATION OF THE ARIMA MODEL TO ANALYZE AND FORECAST THE TIME SERIES OF DENSITY CORRECTIONS FOR NRLMSIS-00 *

Vasiliy S. YURASOV1, Andrey I. NAZARENKO2, Paul J. CEFOLA3, Kyle T. ALFRIEND4

1 Chief of Department, Space Informatics Analytical Systems (KIA Systems), Gjelsky per. 20, 105120, Moscow, Russia
2 Chief Scientist, Space Observation Center, 84/32 Profsoyuznaya ul, 117810, Moscow, Russia
3 Consultant in Aerospace Systems, Spaceflight Mechanics, and Astrodynamics, Sudbury, MA, USA [also Research Affiliate, MIT Department of Aeronautics and Astronautics]
4 TEES Distinguished Research Chair Professor, Texas A&M University, 701 H. R. Bright Building, Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843-3141, USA

Abstract. Previously the authors described a technique for estimating the fluctuations between the actual atmosphere density and a chosen atmosphere density model. The observation data is the Two Line Element set data associated with catalogued inactive payloads and debris. Time-series for the density corrections for the Russian operational GOST atmosphere density model and for the US NRLMSIS-00 atmosphere density model were constructed over a four-year interval.
In this paper, the authors investigate the basic statistical properties of the observed density corrections for the NRLMSIS-00 model. The following are provided:
  • Statistical distributions of the b1 and b2 density correction coefficient time series along with distributions of the solar activity and the geomagnetic index
  • Correlations (with scatterplots) between the b1 and b2 time series, as well as with the solar activity and the geomagnetic index time series
  • Autocorrelation functions for the b1 and b2 time series, and the solar activity and the geomagnetic index time series, for various lag times
  • Cross correlation functions
These results suggest that time series analysis techniques may be applied to identify the nature of the phenomena represented by the time series of the density correction estimates and for their forecasting. The matrix autoregression equations for the parameters of the density corrections are constructed in order to reveal the time regularities of the density correction parameters, and to allow more efficient prediction of the density correction parameters.
The Autoregressive Integrated Moving Average (ARIMA) method is used to construct simple scalar models describing the b1 and b2 time series of density corrections for the NRLMSIS-00, to smooth them, and to predict the future values of the time series using observations up to the current time. The ARIMA model represents the time series values observed at the given time instant as a linear combination of previous values of the series and a linear combination of moving averages. The ARIMA methodology was developed by Box and Jenkins. It has gained enormous popularity in many areas of research. The selection of the ARIMA model parameters, which adequately describe the behavior of the analyzed b1 and b2 time series of density corrections, was carried out by enumerating a set of test models. The accuracy of the density correction forecasting for the NRLMSIS-00 model was estimated using an ARIMA (6,1,6) model.
_______________________________
* This work was undertaken under an agreement between the Texas Engineering Experiment Station (ref. #D40006) and Prof. A. I. Nazarenko from the Space Observation Center, Moscow, Russia.
1. INTRODUCTION

Atmospheric density mismodeling was, and remains, the dominant error source in the orbit determination and prediction of LEO satellite orbits. To improve the accuracy of motion prediction for these satellites, it has been proposed to track the actual density of the upper atmosphere using the available drag data on the catalogued LEO satellites. The total number of such drag-perturbed Space Objects (SOs) reaches several hundred at any given time. The element sets for these SOs are updated as an ordinary routine operation by the space surveillance systems. We use these element sets as the observation data for estimating the corrections between the actual atmosphere density and a chosen atmosphere density model. Recently we obtained the density corrections for the NRLMSIS-00 atmosphere model using the Two Line Element sets (Ref. 1). Time series for the density corrections were generated on a one-day grid over a four-year interval from December 1, 1999, to November 30, 2003. Fig. 1 illustrates the time histories of the estimated correction parameters b1 and b2 for the NRLMSIS-00 density model. Using these data, everyone can independently estimate the corrections to the NRLMSIS-00 model density and take them into account in orbit calculations by the formula

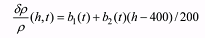           (1)

The effectiveness of this process was evaluated by comparing the orbit determination and prediction results obtained without and with the constructed density corrections. The application of density corrections for the NRLMSIS-00 model reduced the scattering of ballistic coefficient estimates from 2 times for eccentric orbits up to 5.6 times – for near- circular orbits. The reduced scattering in the ballistic coefficient values indicates that the various complexities in the physics of the atmosphere are more consistently modeled with the density corrections (Ref. 2).

In the current paper, the initial emphasis is on the basic statistical analysis of the considered parameters (density correction parameters and solar activity and geomagnetic index). The longer term goal is to develop relationships of the form:

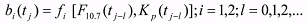           (2)

The following are provided:
  • Statistical distributions of the b1 and b2 density correction coefficient time series along with distributions of the solar activity and the geomagnetic index
  • Correlations (with scatterplots) between the b1 and b2 time series, as well as with the solar activity and the geomagnetic index time series
  • Autocorrelation functions for the b1 and b2 time series, and the solar activity and the geomagnetic index time series, for lag times of 1 day through 30 days
  • Autocorrelation functions for the b1 and b2 time series for lag times of 16 days through 365 days
  • Cross correlation function of the b1 and b2 parameters
  • Cross correlation function of the solar activity and the b1 parameter
  • Cross correlation function of the geomagnetic index and the b1 parameter
  • Cross correlation function of the solar activity and the b2 parameter
  • Cross correlation function of the geomagnetic index and the b2 parameter
  • Cross correlation function of the solar activity and the geomagnetic index

Next the construction of the matrix autoregression equations for the parameters of density correction and the application of these equations for forecasting the density correction is considered.

Finally the application of the ARIMA model to analyze and forecast the time series of density corrections is considered.
2. STATISTICAL PROPERTIES OF THE DENSITY CORRECTION TIME SERIES FOR THE NRLMSIS-00 MODEL

Figure 1 presents plots of the time histories of the b1 (‘blue’) and b2 (‘black’) coefficients for the density corrections in the NRLMSIS-00 model. The data processing technology used to generate the NRLMSIS-00 density corrections (Refs. 3 thru 6) is similar to that used previously for the GOST density model. The only distinctions were:
  1. The Everhart numerical method (Refs. 7, 8) was used for satellite motion propagation instead of the Universal Semianalytical Method (USM).
  2. The osculating orbital elements, generated from TLE sets, were used as the measurements in the secondary data processing instead of the USM mean elements.
  3. The 81-day averages of F7,10 values, centered on the day of interest, were used instead of weighted-average values of solar activity index F7,10 for the preceding 81 days, which were applied in the GOST model.
  4. The daily magnetic indices Ap were used in the NRLMSIS-00 model instead of mean diurnal indices Kp in the GOST model.
  5. Different values of delays for the solar activity and geomagnetic index (F7,10 and Ap) are used in the NRLMSIS-00 and GOST models.

In total, 1460 daily estimates of each of the b1 and b2 parameters were obtained. Figures 2 and 3 give the solar activity and geomagnetic index data for the time interval. Further details regarding the construction of the density corrections for the NRLMSIS-00 density model are given in the authors’ previous paper, Ref. 1.

The natural approach to construction of mathematical models is based on obtaining, accumulating, and analyzing data on the evolution of the object’s state in time when these data are accessible to measurement. In this, we follow the overall approach of Box and Jenkins (Ref. 9).

Figures 4 to 7 show the statistical distribution of the observed estimates of the b1 and b2 density correction coefficients, as well as the solar activity and the geomagnetic index. These distributions, except for Figure 7 for the geomagnetic index, are close in their form to normal distributions. This implies the possibility of applying both the statistical methods developed for random values having normal distribution, and the linear relations between considered parameters.

Figures 8 through 12 give scatterplots for various pairs of the considered parameters. The least-squares regression line is also presented in each of these plots. It is seen from Figure 8 that a significant correlation exists between the b1 and b2 parameters. The greater the positive value of the b1 coefficient, the stronger the increase of density correction with altitude (b2). At the same time, it is seen from Figure 9, that the relation between the b1 values and the solar activity variations is weak. Similarly, Figure 10 shows that the relation between b2 and the solar activity variations is weak. Figure 11 shows that the correlation of the b1 values with the geomagnetic index variations is weak. Figure 12 shows that the correlation of the b2 values with the geomagnetic index variations is also weak.

The previous data are characterized by the fact that they do not take into account the time relations between the parameters. We now consider the relations between the analyzed time series data, namely their auto correlation and cross-correlation functions. The autocorrelation is the correlation of a series with itself lagged by a particular number of observations. The auto correlation at lag k is (Ref. 9, p. 26):

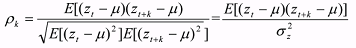           (3)

where

           

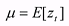and

           

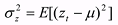The auto correlation at zero lag is one.

Figures 13 and 14 give the autocorrelation of the b1 and b2 series, respectively. The lag values in these figures are plotted on the vertical axis for lags from one (1) to thirty (30) days. A common feature of these functions is the presence of a local maximum in the area of lag values of 25 to 29 days. This effect is a natural manifestation of the well-known monthly cycle of solar activity influencing the state of the upper atmosphere.

Figure 15 gives the autocorrelation of the difference between the daily value of the F10.7 solar activity and the 81 day average F81. Figure 16 gives the autocorrelation for the geomagnetic indices Ap.

The b1 and b2 time series have very large values of autocorrelation coefficients for lags less than 7 (seven) days. They exceed the value of 0.7. The corresponding values for the solar activity and geomagnetic index are much lower. This circumstance suggests the possibility of developing rather efficient algorithms for short-term forecasting of the b1 and b2 future values.

Figures 13 and 14 (b1 and b2 series) show plots of the autocorrelation functions for the maximum lag of 30 days. Let us consider now similar plots constructed for the maximum lag of 365 days. These plots are shown in Figures 17 and 18. The annual effects in the corrections to atmospheric density, constructed for the NRLMSIS-00 model, are well seen in these plots. The maximum values of semi-annual correlations the b1 and b2 parameters are equal to -0.384 and -0.379, respectively. The values of the annual correlations for these parameters are equal to 0.296 and 0.422. All these data indicate that the given model poorly represents the monthly and annual changes of density in the upper atmosphere, and show possible directions for its improvement.

The data analysis tool employed for the identification of transfer function models is the cross correlation function between the input and output (Ref. 9, Chap. 11). The cross correlation function at lag k is given by

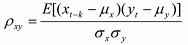           (4)

where μx and μy are the corresponding expected values for the two time series and σx and σy are the respective standard deviations.

The cross correlation functions of the considered parameters are presented in Figures 19 through 24. Based on the presented cross correlation functions, one can draw conclusions on the possibility of developing an algorithm for forecasting density correction coefficients for the NRLMSIS-00 model using their previous values.

The cross correlations of the b1 and b2 time series are significant for the NRLMSIS-00 model. Values of the cross correlation coefficients exceeding 0.50 were revealed for the NRLMSIS-00 model on lags of +/-9 days and on the monthly lag.

The cross correlations of the b1 and b2 series with solar activity were much smaller.

The cross correlations of the b1 and b2 series with the geomagnetic index are also much smaller.

Similar statistical data for the GOST atmosphere density model (Ref. 10) also have been obtained. These results are given in Ref. 11.

Overall, the given results for NRLMSIS-00 suggest the urgency of application of time series analysis techniques for identifying the nature of the phenomena represented by the time series of density correction estimates and for their forecasting (the prediction of future values of the b1 and b2 time series).
3. THE USE OF AUTOREGRESSION EQUATIONS FOR FORECASTING THE DENSITY CORRECTION PARAMETERS

The technique for constructing the autoregression equations for vectorial processes was presented in Section 3.4 of Ref. 12 and in Ref. 13. The intent is that using this technique will make it possible to reveal the time regularity of the considered parameters, which will allow for more efficiently predicting the parameters as compared to the case of using simplified methods. In the case, where the state of some object (in our case - the atmosphere) at any time instant is characterized by some vector, and the time series describing the change in the state vector are stationary, the mathematical model of the objects can be represented as a vector autoregression process of the type

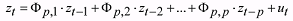           (5)

Here: a) zt is the n-dimensional vector, b) Ôp,j, j=1, …, p are the n-dimensional matrix coefficients of the autoregression process, and c) ut is the vector of a random variable.

As the state vector components we shall consider the values of the b1 and b2 parameters of density corrections, as well as the values of solar and geomagnetic activity indices (F7.10 and Kp). Thus, in our case the state vector zt is 4-dimensional one. Its values are known on the same time interval with the step of 1 day. They are presented in Figures 1 through 3 of this paper. Below, in analyzing solar activity, we shall consider the difference of the current F7.10 index value and the 81-day running average centered on the day of interest (F81).

As the initial data for forecasting we have used the set of values of density correction parameters b1 and b2, as well as the values of solar and geomagnetic activity indices presented in Figures 1 through 3. The statistical characteristics of state vector components are presented in Table 1.

Table 1. Statistical characteristics of state vector components

Characteristic Components of the state vector (z)
# 1 2 3 4
Designation b1 b2 F7.10 - F81 Kp
E(z) -0.0014 0.00390 0.043 2.41
SD(z) 0.1510 0.1017 26.14 1.141

The values of autoregression matrix factors of the second order, Ô1,2 and Ô2,2, were presented in Ref. 11. The formulas are:

           (6)

           (7)

We note that the matrices given in Equations (6) and (7) are specific to the specific four year interval and the choice of the NRLMSIS-00 density and the specific parameterization of the solar activity and geomagnetic index data.

The standard method for determining the matrix coefficients Ôp,j is based on the construction and solution of the so-called Yule-Walker equations (Ref. 9). The solution of the Yule-Walker equations in the explicit form (see Equation 3.2.7 in Ref. 9) is not always convenient because of difficulties associated with the matrix inversion of high dimension. More convenient is the recurrent solution procedure, which allows one to obtain the solution at the (p+1)th step using the results of the pth step. Such a procedure is developed for vector processes and described in Ref. 13.

The forecasting is carried out, based on the model given in Equation 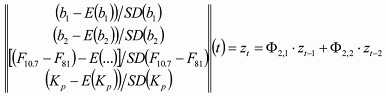(8).

           (8)

Forecasting was carried out using Equation (8) according to two distinct test protocols:
  1. The known values (zt - 1 and zt - 2) of a state vector at two points were used as the initial data. 1450 versions of the initial data were applied. They were selected from the mentioned set of known values with a moving shift of 1 day. The forecasts were carried out on an interval up to 10 days. In forecasting for one step, after carrying out calculations by Equation (8), the moving shift of state vector components was made: (zt - 2)new = zt - 1, (zt - 1)new = zt.
  2. The known values (zt - 1 and zt - 2) of a state vector at two points were selected only once - for time instants t = December 10 and 11, 1999. Further, at each step of forecasting, the known values of solar and geomagnetic activity indices, plotted in Figures 2 and 3, were used as the initial data. The shifting of the state vector ((zt - 2)new = zt - 1, (zt - 1)new = zt) was carried out only for the components of vector z related to the b1 and b2 parameters of density corrections. The forecasting interval equals 1450 days.

The normalized forecasting errors were calculated for each predicted point using the following equation:

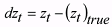           (9)

The mean values and the standard deviations of the normalized forecasting errors were calculated based on the accumulated values of the normalized forecasting errors.

Comment. The first version of forecasts relates to the conditions of applying the current known estimates of b1 and b2 parameters of density correction, as well as of solar and geomagnetic activity indices for short-term forecasting of atmospheric density. Such calculations characterize the efficiency of application of density corrections for solving the operative ballistic tasks. The second version of forecasts allows for estimating the possibility of application of the autoregression equations (8) under the conditions of absence of current estimates of b1 and b2 parameters of density corrections. It is based on using the current estimates of solar and geomagnetic activity indices only. The results of such calculations characterize the possibility of application of the autoregression equation (8) as an addition to the atmosphere model. They are based only on using the found dependences of b1 and b2 parameters on solar and geomagnetic activity variations.

Table 2. Statistical characteristics of normalized errors

Forecasting
interval,
days		 Mean values Standard deviations
b1 b2 F10.7 Kp b1 b2 F10.7 Kp
1 0.0008 0.0007 0.0002 0.0009 0.1745 0.2880 0.3682 0.8283
2 0.0015 0.0023 -0.0001 0.0027 0.2969 0.3959 0.5368 0.9633
3 0.0017 0.0021 -0.0008 0.0040 0.4281 0.5054 0.7019 0.9885
4 0.0016 0.0013 -0.0021 0.0030 0.5286 0.5822 0.8388 0.9925
5 0.0015 0.0005 -0.0031 0.0026 0.6132 0.6519 0.9533 0.9943
6 0.0015 -0.0003 -0.0043 0.0023 0.6778 0.7086 1.0402 0.9956
7 0.0020 -0.0003 -0.0053 0.0019 0.7357 0.7578 1.1075 0.9965
8 0.0029 0.0006 -0.0062 0.0016 0.7822 0.7989 1.1533 0.9975
9 0.0036 0.0023 -0.0071 0.0009 0.8203 0.8330 1.1837 0.9985
10 0.0046 0.0030 -0.0080 0.0008 0.8452 0.8569 1.1994 1.0010

For the first version of the test protocol, the basic forecasting results (the statistical characteristics of normalized errors) are presented in Table 2 and in Figure 25. It is seen from these data that for forecasting intervals up to 4 days the SD of normalized errors of b1 and b2 parameters change nearly linearly in the range of values from (0.2-0.3) to (0.5-0.6). The errors in the forecasting of the solar activity are slightly greater. For the geomagnetic index, the corresponding characteristics vary from 0.80 to 1.0. It is natural that, later on, as the forecasting interval increases, the SD of normalized errors of all parameters tends to the value of 1.0. The average values of normalized errors in all cases are much lower, than the standard deviations.

Thus, the presented results testify to a rather high efficiency of the application of the vectorial autoregression equations for short-term (up to 4 days) forecasting of density corrections. As compared to forecasting without density correction (SD(…)=1.0), the errors of calculations of b1 and b2 parameters decrease 2-5 times for the forecasting interval of 1 day and 2 times – for the forecasting interval of 2 days. For forecasting intervals of 10 days, the application of the autoregression equations results in about 15% decrease in the errors as compared to calculation versions without density corrections.

Figures 26 and 27 show examples of forecasting the b1 and b2 parameters and their comparison with accurate (known) values. The data of these figures demonstrate the possibilities of application of the autoregression equations for forecasting these time series. The account taken of previous values of the state vector (in this case - for two time instants) and general (averaged) statistical laws does not allow the prediction of the random (not regular) variations of parameters.

In carrying out calculations by the second version of the test protocol, the forecasting results for the first 100 steps after starting were not included in the statistical error data, Equation (9). The statistical characteristics of the normalized errors (the average values and standard deviations) were determined on the basis of forecasting results related to the time interval beginning 110 days after starting (1350 realizations).

Figures 28 and 29 show the results of forecasting both the b1 and b2 parameters and comparison of the forecasts with the corresponding true data. One can see from the presented results that, on the average, the forecasted values of parameters are lower than the observed variations. Besides, in some cases, essential divergences between their general behaviors are observed. In particular, in June-August of years 2001 and 2002 the forecasted values of parameter b2 are positive, whereas the observed (true) values are negative. However, such a divergence is absent in the data for year 2003: rather good agreement is observed in this case.

As an example, for the time interval from November 15, 2002, to January 14, 2003, the corresponding results are presented in Figures 30 and 31 in a larger scale. These data show once again, that the forecasting of b1 and b2 parameters without taking into account their current estimates (i. e. based on the data on solar and geomagnetic activity only) does not allow one to obtain an acceptable agreement between the predicted and true values. Table 3 shows the summary statistical characteristics of forecasting results.

For correct interpretation of the Table 3 data one should remember that the estimates of b1 and b2 parameters were determined by means of long-term forecasting, whose results depend on the current values of solar and geomagnetic activity only. The forecasting of F7.10 and Kp parameters was carried out for one step (1 day) only. After this, the true values were used as the initial data for forecasting. So, the statistical characteristics for these parameters were obtained by forecasting for 1 day.

Table 3. Statistical characteristics of normalized errors (Case 2)

  Mean values Standard deviations
Parameters b1 b2 F10.7 Kp b1 b2 F10.7 Kp
Estimates 0.0262 0.0202 -0.0008 -0.0089 1.1038 1.0128 0.3691 0.8252

The following conclusions arise from the results of the second version of calculations:
  1. The application of the autoregression equations (8) under the conditions of absence of current operative estimates of b1 and b2 parameters of density corrections does not result in increasing the accuracy of atmospheric density calculation as compared to calculations without density correction. In this case the SD of normalized errors of b1 and b2 parameters are close to 1.
  2. The result mentioned in item 1 can be explained by the fact, that there is an essential random component in the variations of the b1 and b2 parameters, which is not taken into account in the autoregression equations. This statement is well illustrated by the data of Figures 28 and 29. It is seen that in many cases abnormally large variations in the density correction parameters were observed, which could not be predicted by calculation results. The vectorial autoregression equations of the second order do not take into account long-periodical patterns of density corrections. It is possible, that the increase of autoregression equation order or some other way of accounting for these patterns will allow reduction in the value of the random component and an increase in the accuracy of the forecasted density corrections. The existence of such capabilities is confirmed in the next section of this paper.
  3. The standard deviations, presented in Table 3 for solar and geomagnetic activity parameters, are in good agreement with corresponding data of Table 2 related to the forecasting interval of 1 day
    4. .
4. APPLICATION OF THE ARIMA MODEL TO ANALYZE AND FORECAST THE TIME SERIES OF DENSITY CORRECTIONS

The task we consider in this section is formulated as follows: to construct simple scalar models describing the b1 and b2 time series of density corrections for the NRLMSIS-00 model, to smooth them and to predict the future values of the time series using observations up to the current time instant. Unlike the previous section, where the autoregression model was used, we now use the ARIMA methodology for the solution of this task. The ARIMA model describes the consecutive elements of the series in terms of specific, time-lagged (previous) elements (the Autoregression hereafter) and a linear combination of moving average values for this time series (the Moving Average hereafter). The ARIMA methodology was developed by Box and Jenkins (Ref. 9). It has gained enormous popularity in many areas and research practice, which confirms its power and flexibility. However, because of its power and flexibility, the ARIMA is a complex technique; so, it is not easy to use it: this requires a great deal of experience, although it often produces satisfactory results. The latter depends on the researcher's level of expertise.

The general model introduced by Box and Jenkins includes autoregressive as well as moving average parameters, and explicitly includes differencing in the formulation of the model. Specifically, the three types of parameters in the model are: the autoregressive parameters (p), the number of differencing passes (d), and moving average parameters (q). In the notation introduced by Box and Jenkins, the models are summarized as ARIMA(p,d,q). For example, a model described as ARIMA(0,1,2) means that it contains 0 (zero) autoregressive (p) parameters and 2 moving average (q) parameters, which were computed for the series after it was differenced once.

Thus, we have to decide, how many (p,d,q) parameters of the ARIMA model are necessary to describe adequately the behavior of observed b1 and b2 time series for the density corrections to the NRLMSIS-00 model. The determination of these parameters for the ARIMA model is based on analysis of the statistical characteristics of the b1 and b2 time series. In particular, the input series for ARIMA needs to be stationary; that is, it should have a constant mean, variance, and autocorrelation through time. Therefore, usually the series first needs to be differenced until it becomes stationary. The number of times the series needs to be differenced to achieve stationarity is reflected in the d parameter. In order to determine the necessary level of differencing, one should examine the plot of the data and the autocorrelogram. Significant changes in the level usually require first-order non-seasonal (lag=1) differencing; the strong changes of a slope usually require second-order non- seasonal differencing. It is seen from the plots in Figures 13 and 14 that the estimated autocorrelation coefficients for b1 and b2 decline slowly at longer lags. In the ARIMA model first-order differencing is usually required in this case. However, one should keep in mind that some time series may require either little or no differencing, and that over differenced series may produce less stable coefficient estimates. Therefore, we shall try to construct the model with first-order differencing.

At the model identification phase we also need to decide, how many autoregressive (p) and moving average (q) parameters are necessary to yield an effective but still parsimonious model of the process. “Parsimonious” means that it has the fewest parameters and greatest number of degrees of freedom among all models that fit the data. Major tools used in the identification phase are plots of the series, the correlograms of the autocorrelation function (ACF), and the partial autocorrelation function (PACF). The decision is not straightforward, and in less typical cases it requires not only experience but also a good deal of experimentation with alternative models. However, the majority of empirical time series patterns can be satisfactorily approximated using one of the 5 basic models that can be identified based on the shape of the autocorrelogram (ACF) and the partial autocorrelogram (PACF). The following brief summary is based on practical recommendations by Pankratz (Ref. 14).
  1. One autoregressive (p) parameter: ACF - exponential decay; PACF - spike at lag 1, no correlation for other lags.
  2. Two autoregressive (p) parameters: ACF - a sine-wave shape pattern or a set of exponential decays; PACF - spikes at lags 1 and 2, no correlation for other lags.
  3. One moving average (q) parameter: ACF - spike at lag 1, no correlation for other lags; PACF - damps out exponentially.
  4. Two moving average (q) parameters: ACF - spikes at lags 1 and 2, no correlation for other lags; PACF - a sine-wave shape pattern or a set of exponential decays.
  5. One autoregressive (p) and one moving average (q) parameter: ACF - exponential decay starting at lag 1; PACF - exponential decay starting at lag 1.
Figure 32 presents the ACF plot of the time series generated by once differencing of the b1 time series with one day lag (D(1)). It is seen that the ACF has a sine-wave shape pattern.

The PACF plot for the same time series is shown in Figure 33. It is seen from this plot, that spikes are observed for various lag values. Therefore, none of models mentioned above is suitable for describing the statistical characteristics of the b1 parameter.

For the initial analysis we choose the model, which can be described as ARIMA(2,1,0) in the ARIMA notation, i.e. p=2, d=1, q=0. For b1 the following estimates and their standard errors for the ARIMA (2,1,0) model parameters were obtained: p(1)=0.42443 (SD=0.02608), p(2)=0.10209 (SD=0.02608). The initial and final sums of squares (SS) are equal to 1.3379 and 1.0282, respectively. The number of observations used to estimate the model parameters was equal to 1458.

All-round analysis of the residuals is necessary for estimating the quality of the constructed model. The qualitative model should have the independent residuals containing a noise without systematic components. In particular, the ACF of residuals should not contain any periodicity.

In Figures 34 and 35, plots of the autocorrelation and partial autocorrelation functions for the residuals corresponding to the ARIMA(2,1,0) model are presented. It is seen from these plots, that the correlation score of the residuals exceeds the confidence level. This means that the model we have chosen describes the observed process inadequately.

For completeness, Figure 36 gives the plot of residuals vs. time, and Figure 37 shows the histogram of residuals distribution. In particular, it is seen from the plot in Figure 36, that a heightened level of residuals was observed in 2003.

Thus, the simple ARIMA(2,1,0) model we have constructed does not adequately describe the observed time series for b1. Let's try to find an alternative model for these data. For this purpose we shall adjust successively the p and q input parameters of the ARIMA model for the fixed value of parameter d=1. For each set of input parameters we shall estimate the model’s parameters using the function minimization procedures. In practice, this requires calculations of the sums of squares (SS) of the residuals because the estimation procedure minimizes the sum of squares of residuals for the model. Therefore, we shall choose the ratio of the final SS value to the initial one as a main criterion for comparison of constructed models for various p and q. The initial SS values are the same for all comparing models. Therefore the lower the value of this quantity, the better is the constructed model. However, it is necessary to have in view in this case, that the qualitative model should be economical and have independent residuals containing only the noise without systematic components.

Table 4 gives the ratios of final SS values to initial ones for various ARIMA(p,1,q) models, which were constructed for the b1 and b2 time series. On the basis of analysis of the presented data and guided by the necessity of selecting an economical model, the ARIMA(6,1,6) model was chosen both for b1 and b2 series.

Table 4. The ratios of final SS values to initial one for various ARIMA(p,1,q) models

# p q Ratio of final
value SS to its
initial value,
%
b1 b2
1 1 0 77.66 100
2 1 1 77.29 99.98
3 0 1 84.86 100
4 2 0 76.85 99.16
5 2 1 73.33 98.33
6 2 2 69.74 97.99
7 3 0 70.67 97.10
8 3 1 70.51 96.57
9 3 2 69.62 96.24
10 3 3 68.77 94.34
11 4 0 70.42 96.56
12 4 1 70.21 96.52
13 4 2 68.68 96.19
14 4 3 68.22 93.96
15 4 4 68.16 93.45
16 5 0 69.92 96.49
17 5 1 69.88 96.47
18 5 2 68.39 95.82
19 5 3 68.16 91.37
# p q Ratio of final
value SS to its
initial value,
%
b1 b2
20 5 4 64.59 93.33
21 5 5 63.92 91.34
22 6 0 69.73 96.42
23 6 1 69.11 96.41
24 6 2 68.41 95.81
25 6 3 68.17 91.35
26 6 4 80.50 93.33
27 6 5 64.33 93.15
28 6 6 63.20 91.92
29 7 0 67.76 96.36
30 7 1 64.90 96.32
31 7 2 64.76 95.77
32 7 3 64.76 91.27
33 7 4 63.62 93.37
34 7 5 63.60 92.51
35 7 6 62.96 92.47
36 7 7 62.85 90.61
37 8 0 67.42 96.12
38 8 1 64.80 92.48
# p q Ratio of final
value SS to its
initial value,
%
b1 b2
39 8 2 64.76 91.26
40 8 3 63.98 91.17
41 8 4 63.60 91.17
42 8 5 63.55 91.09
43 8 6 62.90 90.94
44 8 7 62.84 89.76
45 8 8 62.05 90.32
46 9 0 67.04 95.38
47 9 1 64.70 92.26
48 9 2 66.11 91.21
49 9 3 63.90 91.17
50 9 4 63.63 89.88
51 9 5 63.45 89.88
52 9 6 62.56 89.72
53 9 7 62.56 89.70
54 9 8 62.01 89.62
55 9 9 61.70 88.85

Table 5 contains the estimates of p(j), q(j) (j=1,2 … 6) parameters for the ARIMA(6,1,6) model, their standard errors (SD) and the t-values (parameter estimates divided by standard errors). These characteristics are given both for b1 and b2 time series. It follows from the presented data, that all obtained estimates of parameters are significant.

Table 5. Parameter estimates for the ARIMA(6,1,6) model for b1 and b2 time series

ARIMA (6,1,6) b1 b2
Parameter
value		 SD t value Parameter
value		 SD t value
p(l) 0.73667 0.068259 10.7922 0.84367 0.180800 4.6663
p(2) 1.08207 0.066714 16.2194 0.67445 0.234040 2.8818
p(3) -1.33270 0.103030 -12.9350 -1.21730 0.117480 -10.3618
p(4) 0.28663 0.085469 3.3536 0.66859 0.125349 5.3338
p(5) 0.61209 0.055192 11.0900 0.49960 0.192759 2.5918
p(6) -0.56948 0.042147 -13.5118 -0.64066 0.124166 -5.1597
q(l) 0.32550 0.070546 4.6141 0.85970 0.195029 4.4080
q(2) 1.00227 0.056831 17.6359 0.58302 0.265672 2.1945
q(3) -0.54355 0.094910 -5.7270 -1.01473 0.133694 -7.5899
q(4) 0.23381 0.063487 3.6828 0.69510 0.116245 5.9796
q(5) 0.22767 0.056132 4.0560 0.33291 0.225198 1.4783
q(6) -0.42958 0.043395 -9.8993 -0.55539 0.155400 -3.5740

Figures 38 and 39 show the ACF plots of residuals corresponding to the case of using the ARIMA(6,1,6) models to describe the b1 and b2 time series. One can notice from the comparison of these plots with those in Figure 34, that the use of the more complicated ARIMA(6,1,6) model has resulted in much less uncorrelated residuals. This means that the chosen ARIMA(6,1,6) model describes the observed time series more adequately. Figure 40 shows the time dependence of b1 residuals for the ARIMA(6,1,6) model. It is seen that, visually, the plot in this figure only slightly differs from the plot for the ARIMA(2,1,0) model presented in Figure 36. The heightened level of residuals since the end of 2002 is noticeable for both models. As to comparison of the dispersion characteristics of residuals for these models, the distribution histogram for b1 residuals, corresponding to the ARIMA(6,1,6) model, is presented in Figure 41. The normal distribution curve is superimposed in the same figure. One can conclude from the comparison of the data of distributions in Figures 41 and 37, that the application of the ARIMA(6,1,6) model has led to a reduction in the spread of residuals by 9% approximately, i. e. from 0.0262 down to 0.0241. The ratio of the SD of the residuals for the ARIMA(6,1,6) model to the SD of the b1 time series (which is equal to 0.1529, see Figure 4) equals about 16%.

Figure 42 plots the time dependence for the b2 residuals corresponding to the use of the ARIMA(6,1,6) model. It is also seen here that the residuals at the end of 2002 and in 2003 are larger than in 2000-2001 years. Apparently, this is due to the influence of the disturbing factors on the estimates of the b1 and b2 values at the end of the analyzed interval. Probably, the ARIMA model would be even more accurate in the absence of these factors. The determination of the nature of mentioned factors requires additional investigations.

The histogram of distribution of residuals for b2 series is plotted in Figure 43. It is seen that this distribution is unbiased. The SD of residuals equals 0.0322. Thus, with respect to the SD of b2 time series (which is equal to 0.1018, see Figure 5), the SD of residuals for the ARIMA(6,1,6) model equals about 32%. This value twice exceeds the ratio for b1 parameter, thus testifying to a lower adequacy of the constructed model for b2 as compared to the model for b1.

Now, when the models are constructed and their adequacy is estimated, it is possible to estimate the quality of the forecasts constructed using these models. The time series of the density corrections for the NRLMSIS-00 model was used as input data for forecasting. One hundred and forty (140) versions of input data were chosen. The initial epoch of each forecast is 10 days later than the previous one. The first forecast starts on January 19, 2000 (the 50th day of considered four-year time period). Each forecast was executed over the interval from one to 10 days.

Figures 44 and 45 give the observed and forecasted values of the b1 and b2 parameters. One can see that the forecasts for the b1 values are slightly more accurate than those for b2.

The errors in the b1 and b2 forecasts were calculated for each forecast point. Their statistical characteristics, mean values and SDs of errors were calculated based on accumulated estimates with the one-day step forecasting interval. The results of these calculations (SD of absolute and normalized errors) of forecasting errors are given in Table 6 and in Figure 46. The dependences of prediction errors for b1 and b2 on the forecasting interval, obtained by the autoregression model described in the previous Section, are also plotted in Figure 46.

It is seen from these data that for forecasting intervals up to 4 days, the SDs of normalized errors of the b2 parameter are identical for the ARIMA(6,1,6) and autoregression models. For the b1 parameter, the ARIMA(6,1,6) model gives a little bit better results, than the autoregression model. The ARIMA(6,1,6) forecasts are better than those of the autoregression model at larger intervals both for b1, and b2. As a whole, the accuracy behavior of these models depends on the forecasting interval. Some distinction in the behavior of SD for normalized errors for b2 in the ARIMA(6,1,6) model can be explained by insufficient number of forecasting statistics.

It is seen from the given data that on forecasting intervals up to 5 days the SD of normalized forecasting errors for density correction parameters increase in the range of values from 0.10 to 0.5. Further, as the forecasting interval increases, the SD of normalized errors continues to be incremented and reach the values of 0.76-0.81 on the 10-day interval. Taking into account the level of errors in estimating b1 and b2 values and the results of previous investigations on the influence of density corrections to the LEO satellite prediction accuracy (Ref. 15), one can assume that, at least on the intervals of about several days, the application of constructed ARIMA models can give noticeable effect in increasing the accuracy of solution of the problems related to LEO satellite tracking.

Thus, the obtained results testify to a rather high operational efficiency of the ARIMA scalar models for short-term forecasting of density corrections. The accuracy of forecasting with using these models exceed the accuracy of vectorial autoregression models by 5-10%.

Table 6. Forecasting error statistics

Forecasting
interval,
days		 SDs of absolute errors SDs of normalized errors
b1 b2 b1 b2
1 0.0216 0.031901 0.141269 0.313371
2 0.0404 0.037969 0.264225 0.372974
3 0.0579 0.050863 0.378679 0.499638
4 0.07129 0.058834 0.466252 0.577933
5 0.07952 0.05727 0.520078 0.562572
6 0.08873 0.06354 0.580314 0.624164
7 0.0967 0.069872 0.63244 0.686361
8 0.1014 0.073359 0.663179 0.720617
9 0.1074 0.076872 0.70242 0.755126
10 0.1161 0.082491 0.75932 0.810322
5. CONCLUSIONS

  1. The statistical analysis of time series of density corrections for the GOST and MRLMSIS-00 atmosphere models was carried out. It was found that the distributions of the corrections coefficients are close to the normal (Gaussian) one. The parameters of a normal probability density function, fitted in the best way to the distribution of b1 and b2 estimates, were found to be close for the GOST and NRLMSIS-00 models (see Table 7)
     
    Table 7. Normal distribution parameters
     
    Density model Normal fit parameters for b1 Normal fit parameters for b2
    Mean SD Mean SD
    GOST 0.0014 0.1472 0.0320 0.1015
    NRLMSIS-00 0.0014 0.1529 0.0040 0.1018
  2. The linear regressions between b1 and b2 time series, as well as the indices of solar and geomagnetic activity, were studied. The most essential correlations were found between the b1 and b2 parameters both for the GOST and for the NRLMSIS-00 models. Namely, the greater the positive values of b1 coefficient, the stronger the incrementing of corrections to density with increasing altitude. And, here, for the NRLMSIS-00 model the degree of this correlation was found to be 1.5 times greater as compared to the GOST model. The dependence of b1 and b2 values on solar and geomagnetic activity indices was observed to be weaker, especially for the NRLMSIS-00 model.
  3. The autocorrelation functions of the b1 and b2 time series were analyzed. It was found that these time series are strongly correlated at small lags. The values of autocorrelation coefficients equal 0.7 or more up to 5 day lags for the GOST model and up to 7 day lags for the NRLMSIS-00 model. The presence of considerable local maximum in the range of 25-29 day lags was found in the correlograms of b1 and b2 time series both for the GOST and NRLMSIS-00 models. For the b1 time series the autocorrelation coefficient in the range of the aforementioned local maximum is almost 1.5 times greater for the NRLMSIS-00 model as compared to the GOST model, and for the b2 time series this coefficient is 1.2 times greater. The autocorrelations of b1 and b2 time series considerably exceed those for solar and geomagnetic activity indices. For the NRLMSIS-00 model the presence of annual periodicity in the correlograms was found. The observed effects can be associated with deficiencies in accounting for monthly and semi-annual effects in density variations in the GOST and NRLMSIS-00 models.
  4. The cross correlation functions of the b1, b2 time series, solar and geomagnetic activity indices were studied. The strong cross correlation between b1 and b2 time series is found at small lags. And, here, it is more considerable for the NRLMSIS- 00, than for the GOST model. The cross correlation between the b1, b2 time series and the solar activity indices was 2-3 times weaker.
  5. The correlation moments of the b1 , b2 time series and the solar activity indices reach maximum (0.2-0.3) values for 5 to 6 day lags. Thereby, the integral effect of the influence of solar activity variations on the atmospheric density is exhibited. The modern atmospheric density models use only the current and 81-day averaged values of solar activity index F10,7. Thus, they do not take into account the mentioned integral effect. Actually, the last 5-6 measured values of F10,7 index can noticeably influence the current density variations, and, so, their accounting can increase the accuracy of density calculation.
  6. Four-, three- and two- dimensional matrix equations, as well as the scalar autoregression equations for density correction parameters of the GOST and NRLMSIS-00 models were constructed.
  7. Estimation of the forecasting accuracy of the density corrections for the GOST and NRLMSIS-00 models using the constructed autoregression equations was carried out. The obtained results testify to a rather high operational efficiency of matrix autoregression equations for short-term (up to 4-5 days) forecasting of density corrections, for the NRLMSIS-00 model especially.
  8. The simple scalar models describing the b1 and b2 time series of density corrections for the NRLMSIS-00 model were constructed using the ARIMA methodology. The ARIMA model represents the time series values observed at the given time instant as a final linear combination of previous values of the series and a linear combination of moving averages. The selection of the ARIMA model parameters, which adequately describe the behavior of analyzed b1 and b2 time series of density corrections, was carried out by the technique of enumerating a set of models.
  9. The accuracy of density correction forecasting for the NRLMSIS-00 model was estimated with using the constructed ARIMA (6,1,6) model. The constructed ARIMA models were found to provide the accuracy of density corrections forecasting, which 5-10% exceeds the accuracy of pure models of vectorial autoregression. The reason of this distinction is the fact, that the vectorial autoregression equations of the second order do not take into account the long- periodical patterns of density corrections. Probably, the increasing of autoregression equation order or some other way of accounting for these patterns will allow to decrease subsequently the value of the random component and to increase the accuracy of density corrections forecasting by using the vectorial autoregression.
6. FUTURE WORK

Possible directions of future activities are as follows:
  1. The extension of the density correction interval to include the multiple 11-year solar cycles. During the given activity we have analyzed the density variations only over a four-year interval and for two atmosphere models. However, for more detailed studying of the accuracies of atmosphere models it is expedient to cover one 11-year cycle of solar activity at least. This problem solution needs to collect, store and process very large volumes of historical data. It can also be aggravated with a planned limitation of access to the TLE data. However, these difficulties most likely have organizational and technical character. At desire they can be solved, and in rather short deadlines, during further joint activities.
  2. Consideration and detailed analysis of data for calibration satellites having spherical shape and known aerodynamic characteristics. During the given activity we have used the data on several satellites of such a type. The results obtained for the NRLMSIS-00 model testify to a high information profit of utilizing the data on calibration SOs. This problem is, however, complicated by difficulties in obtaining reliable data on many of such satellites. Nevertheless, the activity of collecting and processing the data on such SOs should be continued. Apparently, it would be even possible to generate a shared data bank of calibration SOs, which could be accessible to all contributors. Similar examples of generating the shared data exist, for example, on laser ranging satellites.
  3. Investigation of the behavior of density corrections in the vicinity of major geomagnetic storms and solar flux changes. In the given activity we have not concentrated our attention on the analysis of results obtained during strong geomagnetic storms. Nevertheless, such storms have regularly been observed. For example, two geomagnetic storms with record levels were observed within the last year. The first storm took place at the end of October - beginning of November, 2003, and second one – at the end of July, 2004. During these intervals the errors in orbit determination and prediction were the greatest. The results of this investigation may be useful in improving the density models.
  4. The atmospheric density correction allows one to find the individual regularities in time variations of SOs’ aerodynamic characteristics. The statistical analysis of ballistic coefficient estimates, obtained with density correction, allows one to reveal the mentioned regularities. It is expedient to organize the operative and regular monitoring of ballistic coefficients for all objects, in which the heightened level of their variations is observed. The elucidation of individual regularities of ballistic coefficient variability opens additional possibilities not only for increasing the satellite forecasting accuracy, but for the control of their motion around the center of masses as well.
  5. Determination of basic statistical properties of density corrections. This activity was started in the last stage of our work, where we have analyzed the statistical characteristics of density corrections over the four-year interval and revealed some rather interesting regularities. These regularities can be some kind of indicators to the directions of further perfecting the atmospheric density models. In this connection, it would be very useful to get statistical properties of density corrections for one or several 11-year's cycles.
  6. Perfection of the algorithms used for constructing density corrections. In the case, if the satellite drag data with high spatial-temporal resolution is available, of interest would be to use more complicated models of atmospheric density corrections. The difficulties lie here in obtaining such information. For this purpose, it is necessary to organize the collection and processing of information on LEO satellites over all their passages through the observation zone of sensors. However, having in view, the expected final results, such an activity should, apparently, become routine for LEO satellites tracking.
  7. Perfection of the technique for density corrections forecasting. The available capabilities of improving the accuracy are associated with accounting for the long- periodical patterns of density corrections and with increasing the order of vectorial autoregression equations.
  8. Comparisons between various approaches to atmospheric density correction with using the SSN data. The first objective is to compare our results with the HASDM ones (Ref. 16). This activity was started in our work (Ref. 15). It is expedient to prolong such an activity in future.
  9. Using our approach, to construct density corrections for other density models (for example, the Jacchia-Roberts model). Apparently, it is expedient also to organize, on a standing basis, the service of monitoring the density corrections to various atmosphere models with using the drag data on LEO satellites. Such a service could publish the current and forecasted values of density corrections to atmosphere models in the near-real time operation mode on the Internet.

Acknowledgement. The authors would like to acknowledge the representatives of the Space Surveillance community in both the USA and in Russia for supporting the USA-Russia Space Surveillance Workshops in 1994, 1996, 1998, 2000, 2003, and 2005. The specific contributions of Dr. Ken Seidelmann (University of Virginia), Prof. Stanislav S. Veniaminov (Scientific Research Center "Kosmos"), and Dr. Felix Hoots (General Research Corporation) in organizing these workshops are noted. These workshops led directly to the collaboration reported in this paper. We are also grateful to David A. Vallado (now at Analytical Graphics, Inc.), Dr. Chris Sabol (USAF/AFRL), Dr. Matthew Wilkens (Naval Postgraduate School), and Mr. Zachary Folcik (MIT) for their continuing interest in this work. We are very grateful to Dr. Thomas S. Kelso (Analytical Graphics, Inc.) for providing the historical TLE sets using his personal WWW service. The Russian authors are grateful to Andrey Bukreev (Head of the Space Informatics Analytical Systems) and Dr. Vladimir Agapov (Keldish Institute of Applied Mathematics) for their current interest in this topic.
REFERENCES

  1. Yurasov, V.S., Nazarenko, A.I., Cefola, P.J., and Alfriend, K. T., “Density Corrections for the NRLMSIS- 00 Atmosphere Model”, 15th AAS/AIAA Space Flight Mechanics Conference, Copper Mountain, Colorado, Jan. 2005, AAS 05-168.
  2. Schutz, B. E., and Tapley, B. D., Orbit Accuracy Assessment for Seasat, Journal of the Astronautical Sciences, Vol. XXVIII, No. 4, pp. 371-390, Oct.-Dec. 1980.
  3. Cefola, P.J., Nazarenko, A.I., Proulx, R. J., Yurasov, V.S. “Atmospheric Density Correction Using Two Line Element Sets as the Observation Data”. AAS/AIAA Astrodynamics Specialist Conference, Big Sky, Montana, August 2003, AAS 03-626.
  4. Nazarenko, A.I., Yurasov, V.S. “Atmospheric Density Correction Using Real Orbital Data”. 17th International Symposium on Space Flight Dynamics, Moscow, June 2003
  5. Yurasov, V.S., Nazarenko, A.I., Cefola, P.J., Proulx, R. J. “Near Real Time Corrections to the Atmospheric Density Model”. Fifth US/Russian Space Surveillance Workshop St-Petersburg, September 2003.
  6. Yurasov, V.S., Nazarenko, A.I., Cefola, P.J., Alfriend, K. T. Results and Issues of Atmospheric Density Correction. 14th AAS/AIAA Space Flight Mechanics Conference, Maui, Hawaii, Feb. 2004, AAS 04-305.
  7. Everhart, E. 1985. An efficient integrator that uses Gauss-Radau spacings.- In Dynam. of Comets: Their Origin and Evolution, Eds. A.Carusl, G.B.Valsecchi, Reidel Publ. Co., pp.185-202.
  8. Everhart E. 1974. Implicit single sequence methods for integrating orbits.- Celest. Mech., vol.10, pp.35-55.
  9. Box, George E. P., Jenkins, G. M., and Reinsel, G. C., Time Series Analysis, Forecasting and Control, 3rd Edition, Upper Saddle River, New Jersey, Prentice-Hall International, Inc., 1994.
  10. Earth’s Upper Atmosphere Density Model for ballistic support of Flights of Artificial Earth Satellites. GOST 25645.115-84, Moscow, Publishing House of the Standards, 1990.
  11. Nazarenko, A.I., Yurasov, V.S., Atmosphere Density Variation Tracking, Report prepared for Texas A&M University, College Station, Texas, Stage 4, August 2004
  12. Yurasov, V.S., Nazarenko, A.I., Analysis of Reentry Time Prediction Errors for Real Satellites. Report prepared for Texas A&M University, College Station, Texas, Stage 2. June 2004
  13. Kravchenko, S. N., and Nazarenko, A. I., “Recurring Method Of The Construction Of Auto Regression Equations For Vectorial Random Processes”, Engineering Cybernetics, Russian Academy of Sciences, No. 1, 1992.
  14. Pankratz, A. (1983). Forecasting with univariate Box-Jenkins models: Concepts and cases. New York: Wiley
  15. Nazarenko, A.I., Yurasov, V.S., Atmosphere Density Variation Tracking, Report prepared for Texas A&M University, College Station, Texas, Stage 3, April 2004
  16. Storz, M. F., Bowman, B.R., Branson, J. I. “High Accuracy Satellite Drag Model (HASDM)”. AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, California, August 2002, AIAA 2002-4886
LIST OF FIGURES

  1. Fig. 1. Estimated b1 and b2 density model correction parameters for NRLMSIS-00
  2. Fig. 2. Current F10.7 values and averaged solar activity indices.
  3. Fig. 3. Values of daily averaged Kp indices.
  4. Fig. 4. Statistics for the distribution of b1 estimates for the NRLMSIS-00 model.
  5. Fig. 5. Statistics for the distribution of the b2 estimates for the NRLMSIS-00 model.
  6. Fig. 6. Statistics for the distribution of deviations of current index F10.7 from its average value (F81).
  7. Fig. 7. Statistics for distribution of geomagnetic indices Ap
  8. Fig. 8. Correlations between b1 and b2 parameters of density corrections for the NRLMSIS-00 model
  9. Fig. 9. Correlations between solar activity variations and b1 parameter for the NRLMSIS-00 model.
  10. Fig. 10. Correlations between solar activity variations and b2 parameter for the NRLMSIS-00 model.
  11. Fig. 11. Correlations between b1 values and Ap indices for the NRLMSIS-00 model.
  12. Fig. 12. Correlations between b2 values and Ap indices for the NRLMSIS-00 model.
  13. Fig. 13. Autocorrelation function for the b1 series.
  14. Fig. 14. Autocorrelation function for the b2 series.
  15. Fig. 15. Autocorrelation function for the solar activity variations ( F7.10 - F81).
  16. Fig. 16. Autocorrelation function for the geomagnetic indices Ap.
  17. Fig. 17. Autocorrelation function of b1 parameter plotted for the maximum lag of 365 days.
  18. Fig. 18. Autocorrelation function of b2 parameter plotted for the maximum lag of 365 days.
  19. Fig. 19. Crosscorrelation function of the b1 and b2 parameters.
  20. Fig. 20. Crosscorrelation function for the solar activity index and b1 parameters.
  21. Fig. 21. Crosscorrelation function of Ap indices and b1 values.
  22. Fig. 22. Crosscorrelation function of solar activity indices and b2 values.
  23. Fig. 23. Crosscorrelation function of Ap indices and b2 values.
  24. Fig. 24. Crosscorrelation function of solar and geomagnetic activity indices.
  25. Fig. 25. SD of normalized errors versus forecasting interval (Case 1).
  26. Fig. 26. The forecast of b1 parameter for the time interval from November 15, 2002, to January 14, 2003 (Case 1).
  27. Fig. 27. The forecast of b2 parameter for the time interval from November 15, 2002, to January 14, 2003 (Case 1).
  28. Fig. 28. True and predicted values of b1 parameter (Case 2).
  29. Fig. 29. True and predicted values of b2 parameter (Case 2).
  30. Fig. 30. True and predicted values of parameter b1 (Case 2).
  31. Fig. 31. True and predicted values of parameter b2 (Case 2).
  32. Fig. 32. ACF for b1: D(1).
  33. Fig. 33. PACF for b1: D(1).
  34. Fig. 34. ACF for residuals of the ARIMA(2,1,0) model for b1.
  35. Fig. 35. PACF for residuals of the ARIMA(2,1,0) model for b1.
  36. Fig. 36. Residuals vs time of the ARIMA(2,1,0) model for b1.
  37. Fig. 37. Distribution of residuals of the ARIMA(2,1,0) model for b1.
  38. Fig. 38. ACF of b1 residuals for the ARIMA(6,1,6) model.
  39. Fig. 39. ACF of b2 residuals for the ARIMA(6,1,6) model.
  40. Fig. 40. Time dependence of b1 residuals for the ARIMA(6,1,6) model.
  41. Fig. 41. Distribution of b1 residuals for the ARIMA(6,1,6) model.
  42. Fig. 42. Time dependence of b2 residuals for the ARIMA(6,1,6) model.
  43. Fig. 43. Distribution of b2 residuals for the ARIMA(6,1,6) model.
  44. Fig. 44. Forecasted and observed data for b1.
  45. Fig. 45. Forecasted and observed data for b2.
  46. Fig. 46. Dependence of normalized errors on the forecasting interval.

Ðàçìåùåí 4 äåêàáðÿ 2006.
Ãëàâíàÿ Íîâîñòè ÏóëÊÎÍ ÐÑÄÁ Îáñåðâàòîðèè Ïóáëèêàöèè About us Êîíòàêò