DENSITY VARIATIONS IN THE UPPER ATMOSPHERE DURING SEVERAL SOLAR CYCLES DETERMINED FROM SATELLITE DRAG MEASUREMENTS

Stephen H. Knowles

Much attention has been paid to the accuracy with which atmospheric models reproduce the atmospheric density, and thus drag, experienced by a satellite. However, there has been relatively little attention paid to the actual range of atmospheric density encountered by an object at various altitude regimes. This distribution is in fact important to satellite orbit designers and maintainers, to satellite catalog designers, and to collision avoidance specialists because it represents the range of parameters to design against. Use of atmospheric models and real-time density measurement can ameliorate this somewhat, but this compensation is imperfect. To the extent this compensation fails, the relative density distribution represents the drag uncertainty that must be designed against. Therefore it was thought of interest to provide as comprehensive an examination as possible of measured drag. The Naval Research Laboratory has recently obtained from Strategic Command element sets and observations from 32 satellites, in many cases going back to the start of the space-faring age. This database has been used by Emmert et all to determine long term mean density fluctuations, and is thus relatively well characterized. This article describes sampling from this database.

The Naval Research Laboratory (NRL) has recently obtained a complete data base of element sets and observations for 32 objects from the USSpaceCom skin-track catalog. The objects were selected to cover as wide as possible a range of altitudes while maintaining as long a time span as possible. In fact it was possible to obtain a perigee altitude range of from 211 km. (approx.) to 900 km with a time span from near the start of the space age to the present. Resource limitations associated with this project necessitated simplifying the data analysis as much as possible. As a consequence, the results described in this article are semi-qualitative, and further work is indicated. However, given the paucity of comparable analysis, this should represent considerable new information. Table I shows the objects discussed in this article. Perigee and apogee are nominal values in 2002. These objects were selected to give a well- observed mid-altitude object (#60), the object with the lowest perigee (6073) and the object with the highest perigee (6073).

NORAD #	Name	Launch	Perigee	Apogee	Inc.	Drag Alt.
60	Explorer 8	10/3/60	370 km	883 km	50	395 km
419	THOR ABS. deb.	6/29/61	745 km	803 km	67	230 km
6073	SL-6 deb.	3/31/72	209 km	4728 km	52	775 km

The 2-line NORAD elsets have attached a drag parameter n dot that is related to atmospheric drag over the orbital fit span. Using these numbers is an alternative to using Space Surveillance Network observations and performing special perturbations integrations over the interval in question. This is in fact what was done for this investigation because of the limited time and resources available. Using n dots has possible disadvantages. The operational fitspan of three days or longer must be accepted, limiting the time resolution. n dot must be related to the inverse ballistic coefficient in order to come up with a density measurement. On the other hand, the operational orbit analyst has already performed the sometimes-crucial function of discarding bad observational data, in a knowledgeable manner. In order to relate n dot to B, the inverse ballistic coefficient, an equation such as that in Emmert et all must be used. However, in order to determine relative mean density over time, which is the object of this contribution, this is not necessary; in this case the values are automatically normalized. This argument also applies to the fact that explicit knowledge of the mean value of B is not necessary.

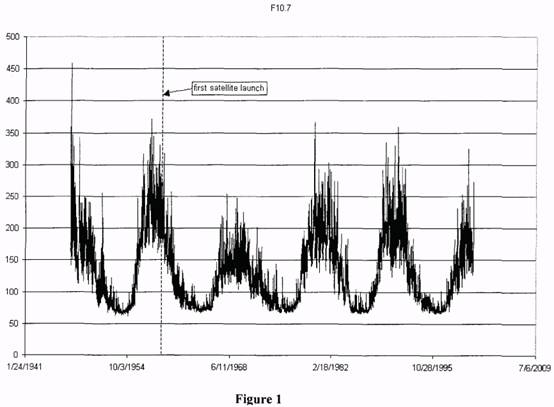
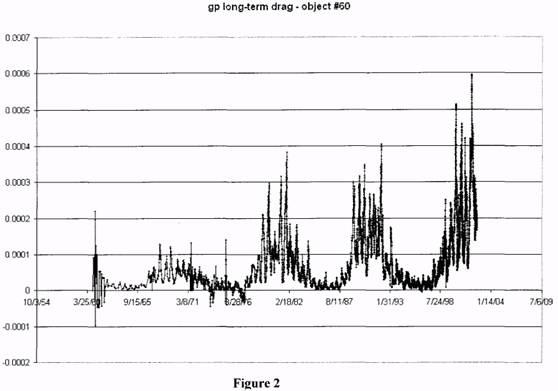
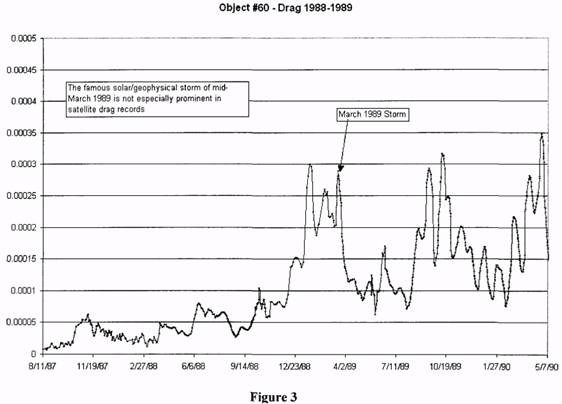
From the time span examined, a comprehensive view of the range of the solar/geophysical indices F10.7 and Ap was available. Figure 1 shows the values of F10.7 over the whole time period this index has been available; also shown is the period available for comparison to satellite drag measurements. Figure 2 shows the value of n dot for object #60 for 1961-2002. This encompasses almost 4 solar cycles. Figure 3 shows that, surprisingly, the drag measured during the well-known event of March 1989 was not significantly greater than other drag peaks. Figure 2 shows a large secular increase in drag. It was obvious from this plot that the secular long-term energy loss (decrease in semi major axis) would need to be compensated for in this analysis. 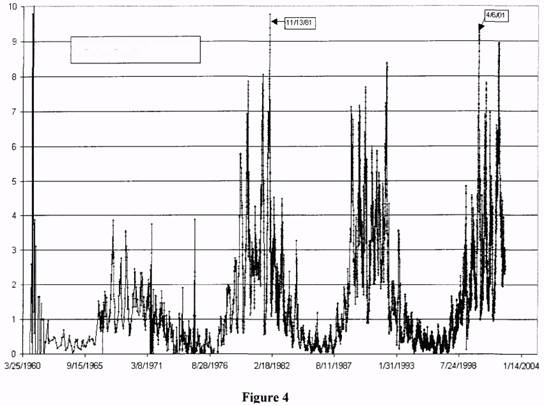This was done by normalizing with respect to the mean density at altitude of date computed from the CIRA-72 model (Valladof A static model was chosen purposely so as not to affect solar cycle variations. 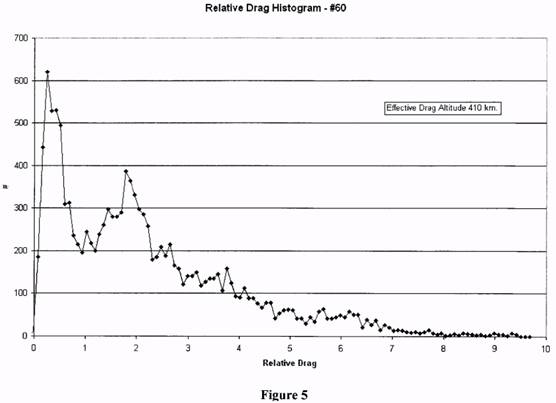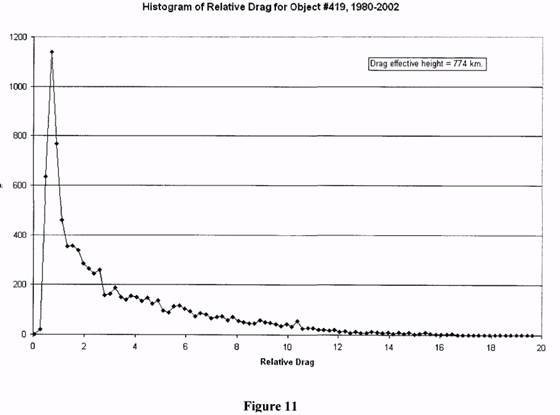When this correction the secular trend in drag vanishes (Figure 4). From the corrected n dots, a histogram was derived of relative drag (Fig. 5). 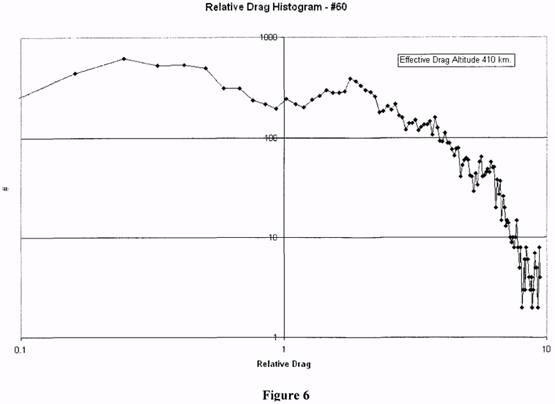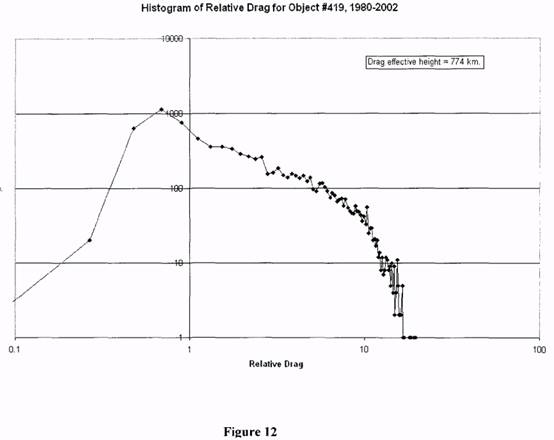Figure 6 displays the same histogram with a log-log scale. The log-log scale is particularly effective in addressing questions of shape of the distribution. With high eccentricity objects the question of the effective altitude for drag purposes must be addressed. The approximation that the effective drag altitude is 1/2 scale height higher than the perigee altitude was used here. The next step was to analyze the data from the object with the lowest perigee.

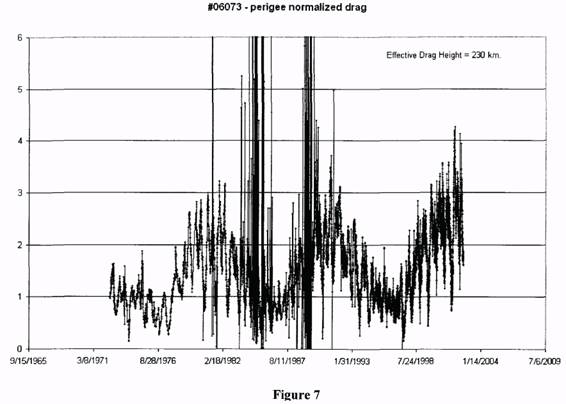
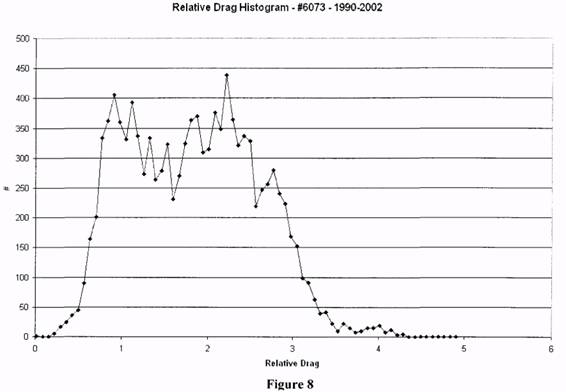
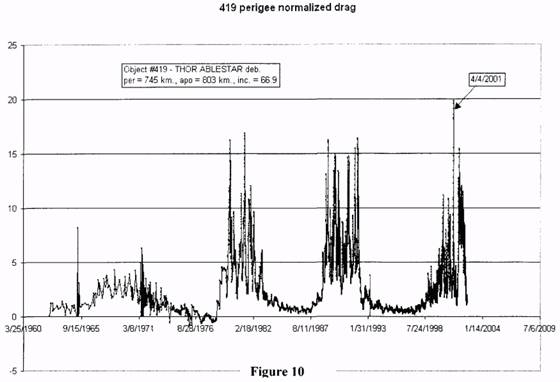
Results for #6073, with an effective altitude of 230 km., are shown in figs. 7-9. Note that in this case only the n dot data from the last solar cycle are of sufficient quality to analyze. Similarly Figs 10-12 show the results for #419, with an effective drag height of about 775 km. Note that the spread of the distribution changes from 3:1 for the lowest altitude to 20: 1 for the highest. This significant effect is expected, and emphasizes the necessity of considering drag variations even at relatively high altitudes. Note also that, at least within the limited historical record, the drag appears to have a “do not exceed” value; that is, it will never be more than a certain amount above the mean.

For all objects examined, the drag during the solar cycle peaking in 1971 was significantly less than in later cycles. This data was eliminated from the histograms, as it was thought it might be related to the change from SGP to SGP4 theory. On the other hand, the 1971 cycle was significantly less active than later cycles, and further analysis is called for to clarify the validity of this data.

This limited-scope investigation has shown that it is possible from available data to provide a synoptic view of mean atmospheric density distribution as a function of altitude. This mean density is the quantity of primary interest to all orbit engineers, bearing directly on questions of lifetime, orbit accuracy, collision avoidance and cataloging. In general, drag results seem to show a maximum density level that is not exceeded, as well as a minimum density level. While the low density limit is expected, the upper density limit is somewhat surprising. The ratio of maximum to mean drag varies from about 3:1 at 250 km. altitude to 20:1 at 900 km. altitude. This higher level of variability at higher altitudes means that monitoring atmospheric density can be important even for objects at altitudes of 1000 km. and above. Within the maximum limit, the density generally follows a power-law distribution. The known major storms (March 1989, Bastille Day 2000, Mar.-ApriI2001) did not produce densities significantly larger than other similar but less notorious events.

This preliminary, limited scope investigation can be extended in a number of directions. Analysis of the Space Surveillance Network observations using a tailored orbit fit would produce a more consistent set of drag data that would hypothetically enable the use of data before 1980 that has been excised for this contribution. It should enable use of shorter fit spans to increase time resolution. The density distribution as a function of phase in the solar cycle should be easily determinable. The inclusion of more objects will increase the statistical validity of the results. Lastly, it should be possible to produce a simple mean density model by simply computing the regression coefficient of drag on F_10.7 and A_p. This model nevertheless would address the principal interest of the satellite engineering community, which is the average drag magnitude over the fitspan.

Размещен 3 декабря 2006.