Ãëàâíàÿ Íîâîñòè ÏóëÊÎÍ ÐÑÄÁ Îáñåðâàòîðèè Ïóáëèêàöèè About us Êîíòàêò
Russian Academy of Sciences
Central Astronomical Observatory at Pulkovo

SIXTH US/RUSSIAN
SPACE SURVEILLANCE WORKSHOP

August 22-26, 2005

Proceedings
Edited by P. Kenneth Seidelmann and Victor K. Abalakin

St. Petersburg, 2005

REVIEW OF RESULTS ON ATMOSPHERIC DENSITY CORRECTIONS*

Vasiliy S. YURASOV2, Andrey I. NAZARENKO3, Kyle T. ALFRIEND4, Paul J. CEFOLA5

2 Space Informatics Analytical Systems (KIA Systems), 20 Gjelsky per, Moscow, 105120, Russia
3 Space Observation Center, 84/32 Profsoyuznaya ul, Moscow, 117810, Russia
4 Texas A&M University, 701 H. R. Bright Building, Department of Aerospace Engineering, Texas A&M University, College Station, TX 77843-3141, USA
5 MIT Aeronautics & Astronautics Department, 59 Harness Lane, Sudbury, MA 01776, USA

Abstract. The main obstructions to increasing the accuracy of orbit determination and prediction for LEO satellites are the errors in the atmospheric density models that are employed. No present-day model can ensure the accuracies required for the solution of many practical space surveillance tasks. Results obtained within the last two years on atmospheric density corrections are reviewed. Previously, it was proposed to use the current drag data for a group of catalogued low Earth orbit (LEO) space objects (SOs) to decrease the errors in the employed atmosphere models. These data allow the construction of operative corrections to the modeled atmosphere density. Using our approach, corrections to the GOST and NRLMSIS-00 atmosphere density models were derived over the four-year interval from December 1999 through November 2003. The density corrections were generated from the smoothed ballistic factors resulting from the secondary data processing. Two Line Element (TLE) sets were used as the input observational data. The potential effect of increasing the accuracy of SO orbit determination and prediction, associated with accounting for the corrections to the GOST and NRLMSIS-00 atmosphere densities, is estimated. The results are of interest not only for orbit prediction tasks but also for perfection of the considered atmosphere density models.
_______________________________
* This work was undertaken under an agreement between Texas Engineering Experiment Station and Prof. A. I. Nazarenko from the Space Observation Center, Moscow, Russia.
1. INTRODUCTION

Atmospheric density mismodeling was, and remains, the dominant error source in the orbit determination and motion prediction of LEO space objects. All known upper atmosphere models describe with insufficient accuracy the real dynamic variations of density caused mainly by the influence of solar and geomagnetic perturbations on the atmosphere.

One promising direction for increasing the accuracy of satellite orbit determination and prediction for low Earth orbit satellites is the real-time estimation and application of density corrections between the real density and the density calculated by the operational atmosphere model. This idea, offered at the beginning of the 1980s [1], is based on the usage of the available atmospheric drag data on catalogued LEO satellites for construction of corrections to the employed atmospheric density model. At any given time there are several hundred such drag-perturbed space objects in orbit. The element sets for these space objects are updated as an ordinary routine operation by the space surveillance systems (SSSs) a few times per day in near-real time. Therefore, corrections to the modeled atmosphere density can be constructed without significant additional costs.

The considered investigations are one of the examples of successful US-Russian cooperative research projects in the area of space surveillance. The beginning of this long- term cooperation was the Second US-Russian Space Surveillance Workshop held in Poznan, Poland in July, 1996. Prof. A. I. Nazarenko presented there a survey paper on this topic [2] and the interesting discussion of these problems took place with Dr. P. J. Cefola.

At the last few US-Russian workshops, discussions on atmospheric density problems have become traditional. Our work on this topic has successfully continued during the two years since the previous workshop at St-Petersburg. The most significant results of these years are the following:
  1. The construction of the density corrections has been described in a mathematically general form.
  2. Software programs and analytical techniques were developed for the construction of atmosphere density corrections using TLE as the observational data.
  3. Density corrections were constructed over four-year intervals for two base models - GOST-25645.115-84 [3] and NRLMSIS-00 [4].
  4. The influence of the density corrections on the orbit fitting and prediction processes for LEO satellites has been investigated.
  5. Obtained estimates for the true values of the ballistic coefficients have been compared with those for the HASDM model and with theoretical estimates.
  6. A comparative estimation of accuracies for the GOST and NRLMSIS-00 density models has been carried out.
  7. Individual regularities in the time variations of SO’s aerodynamic characteristics have been investigated.
  8. Statistical regularities in changes of the density corrections have been investigated.
  9. A technique for forecasting the atmospheric density corrections has been formulated and demonstrated.
This paper is devoted to the review of the results enumerated only in the first seven items. The last two problems from this list will be considered in detail in the other joint paper presented by Dr. Paul Cefola [5].
2. MATHEMATICAL STATEMENT

The estimation of un-modeled variations or the construction of atmospheric density corrections using the available drag data for LEO space objects can be expressed in a general form as a problem of functional minimization [6]

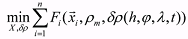         (1)

where n is the number of LEO SOs, chosen for the estimation of density corrections; xi represents the ith SO state vector (i=1 thru n); X (x1, x2, ... xn ); Fi is the optimization criterion, applied to the ith SO for estimation of its motion parameters; ρm = ρm(h,φ,λ,t) is the density calculated by the employed (base) atmosphere model (modeling density value); δρ(h,φ,λ,t) is the density correction function; h is altitude, φ is latitude, λ is longitude, t is time.

The knowledge of density corrections δρ(h,φ,λ,t) allows the calculation of the real values of the density at a point of interest in space

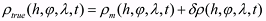         (2)

To solve the minimization task (1) in the general case, the orbit determination process and the density correction process should be considered as a single estimation process. Searching for optimum estimations for the multi-parameter task (1) is a nontrivial problem. Apparently, its correct solution is possible only in the presence of measurements meeting certain requirements on precision, quantity, and spatial and temporary distribution. In our approach, these processes are separated. In addition, due to the difficulty in observing the functional relation of the density corrections to the latitude and longitude by using the available satellite drag data, the density corrections were expressed only as a linear function of altitude

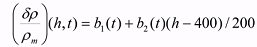         (3)
3. TECHNICAL APPROACH AND SOFTWARE

We have chosen the US SSS TLE data as a basic source of orbital information for the construction of the atmospheric density corrections [7–12]. The choice of the TLE data is explained, first, by their availability over the Internet, and, secondly, by the convenience of obtaining both retrospective, and current TLE-orbits. Moreover, the current orbits are accessible in a near-real time mode.

The satellite drag data, contained in the TLE-orbits, can not be directly used for constructing the density corrections. For this reason, a special algorithmic approach and software were developed for the automated data processing. The process of estimating the density corrections based on the TLE data includes the following basic steps (see Fig. 1).
  1. Choice of a list of LEO satellites on which gathering and processing of the information is carried out. In this choice we were guided by the necessity of obtaining a representative sample of daily satellite drag data distributed over the range of altitudes from 200 up to 600-700 km and over the chosen time interval of processing. During the long duration experiment, the altitudes of some satellites decreased significantly. Some of the chosen SOs decayed due to the atmospheric drag. Therefore, additional SOs were added to the list of chosen SOs to avoid the violation of the data distribution requirements.
  2. The subset of calibration satellites are singled out among the list of chosen SOs. First of all, the satellites of spherical shape, having known mass and size characteristics, are included in this subgroup. The drag data for calibration SOs are used for revealing and estimating the biases, which exist in the base atmosphere models. It can be required also to include new satellites in the subset of calibration Sos, if the duration of experiment is very long.
  3. Gathering and accumulation of orbital data for the chosen SOs. Each of the TLE-format element sets are transformed into mean and osculating elements [7]. All the transformed data are stored in a specially created database and are considered as ‘measurements’ in subsequent ‘smoothed’ orbit and associated ballistic coefficient calculations. The main sources of TLE data were the NASA/GSFC Orbital Information Group [13] and CelesTrak [14] web sites.
  4. Gathering and accumulation of the indices of solar and geomagnetic activity. Values of these indices are used as input parameters in the base atmospheric models. Solar and geomagnetic data also are accessible now in near-real time mode [15].
  5. Estimation of the smoothed orbits and the associated ballistic coefficients. This least squares fit process is called ‘secondary data processing’. It employs the actual values of input parameters for the base density model. It is an a posteriori process. Each smoothed orbit is predicted forward to the epoch of newer ‘measurements’, which have been not used for smoothed orbit determination. The prediction errors along the track are calculated by comparison of the predicted orbit with ‘measurements’.
  6. The density corrections are estimated based on the smoothed ballistic coefficients obtained as a result of the secondary data processing (step #5).
  7. Similar to step #5, the smoothed orbits and associated ballistic coefficients are determined a second time for each epoch of the "measurements" by taking into account the observed corrections in the atmospheric density (step #6). The prediction errors along the track are calculated also by taking into account the density corrections.
  8. The results without density corrections (step #5) are compared to those obtained when the density corrections are included (step #7).

Fig. 1. Steps in the Construction and Test of the Density Corrections.
4. DENSITY CORRECTIONS FOR THE GOST AND NRLMSIS-00 MODELS

The described technique has been applied to two base atmosphere density models – GOST and NRLMSIS-00 [9–11]. Time series for the b1 and b2 coefficients of the density corrections model (3) for these models have been constructed on a one-day grid over the four-year interval starting from December 1, 1999.

The corrections for the GOST model have been calculated using drag data on about 500 SOs. The daily number of estimates of the smoothed ballistic coefficients used for the estimation of the b1 and b2 coefficients varies mainly from 400 up to 600. Almost 800, 000 estimates of the ballistic coefficients were used for the density corrections generated over the four-year interval. Fig. 2 gives for the GOST model the time histories of the estimated b1 and b2 density model correction parameters defined in equation (3).

Due to the great volume of required calculations, only 16 carefully chosen SOs have been used for construction of density corrections for the NRLMSIS-00 model. In 92% of the NRLMSIS-00 cases, the daily number of ballistic coefficient estimates varies from 10 to 25. The total number of ballistic coefficient estimates, obtained on these SOs for the four-year time interval was 24,773. Fig. 3 illustrates the time histories of the estimated correction parameters b1 and b2 for the NRLMSIS-00 density model.

Using the obtained data everyone can independently estimate the corrections to the GOST or NRLMSIS-00 model and take them into account in calculations by formula (3).

As an example, the atmospheric density corrections to the NRLMSIS-00 model, calculated for 2003, are given in Fig. 4 for altitudes of 200, 300, 400, 500 and 600 km. From the presented plots it is visible, in particular, that the larger the height, the larger are the differences between the real values of density and those calculated by the base model. So, the maximum values of atmospheric density corrections for the NRLMSIS-00 density model reached 25% at the 200-km altitude and 70% - at the 600-km altitude. Similar dependence of the density corrections on altitude is observed also for the GOST model results.

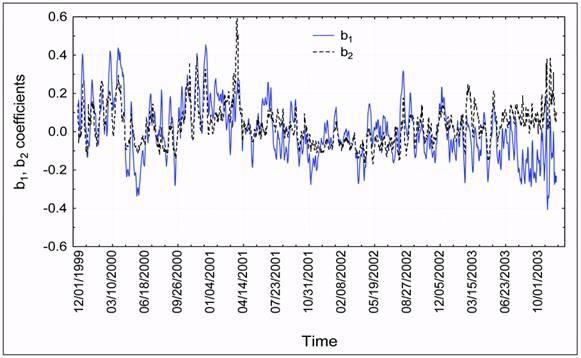Fig. 2. Estimated b1 and b2 density model correction parameters for the GOST model.

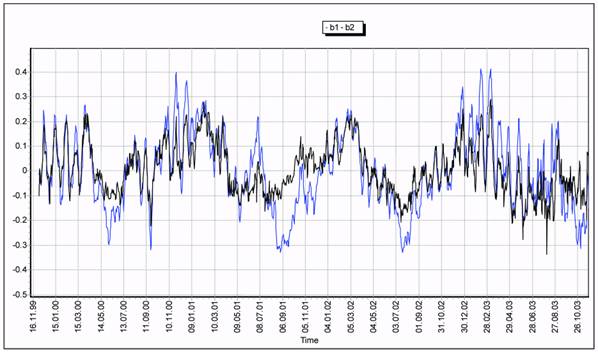Fig. 3. Estimated b1 and b2 density model correction parameters for the NRLMSIS-00 model.

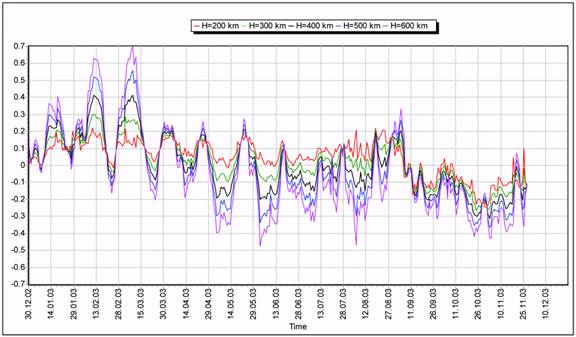Fig. 4. Corrections to the NRLMSIS-00 model for 2003.
5. EVALUATION OF APPLYING THE DENSITY CORRECTIONS

The quality of the constructed density corrections to the base atmosphere model may be evaluated by the comparison of the scatter of the orbit fitting ballistic coefficient estimates obtained with and without the corrected densities. If the density corrections take into account correctly the un-modeled density fluctuations, then the resulting ballistic coefficients for spherical-shaped objects should have significantly smaller scatter. The results presented for the Starshine 3 satellite in Fig. 5 confirm this regularity. Before the density correction the standard deviation (SD) of ballistic coefficient values was 12.8% for this satellite. After applying the density correction, the standard deviation decreased down to 2.8%. For the NRLMSIS-00 model such comparisons have been carried out for 25 SOs, of which 9 SOs were not included in the list chosen for the density correction process. Fig. 6 presents the scatterplot of ballistic coefficients estimates for all SOs, obtained without (Kb-variations) and with (Kbf-variations) density corrections taken into account. The analysis of these data indicates that the application of density corrections to the NRLMSIS-00 model has eliminated the long-periodic variations in the ballistic coefficient estimates caused by the errors in the atmospheric density model. On the average, the density corrections to the NRLMSIS-00 model reduced the scattering of the ballistic coefficient estimates by a factor of 3.6.

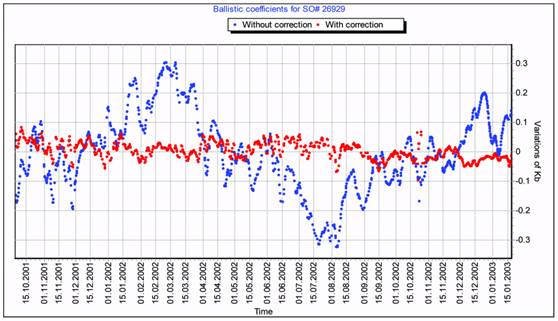Fig. 5. Ballistic coefficient variations obtained for Starshine 3 satellite without and with density correction (GOST)

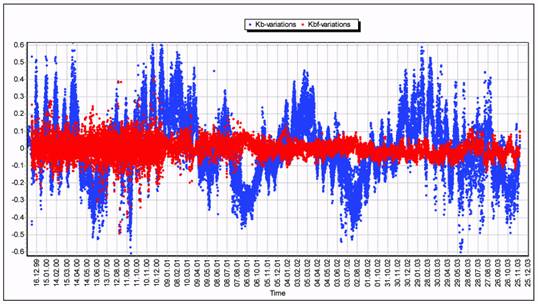Fig. 6. Variations of ballistic coefficients before and after applying the density model correction (all 25 SOs) (NRLMSIS-00).

The comparative analysis of variations of ballistic coefficients obtained before and after density corrections has been fulfilled for the GOST model also. The generalized statistical characteristics of the distribution of variations for this model are presented in Table 1. The comparison interval includes data over the entire four-year interval, from December 1999 through December 2003. The results of the data processing over this interval have shown that the SD of ballistic coefficient variations, estimated for all SOs without atmospheric density corrections, was equal to 23.4%. The number of estimates of the ballistic coefficients was equal to 794,906. For the calibration SOs these values were equal to 15.8% and 97,881 respectively. The SD of ballistic coefficient variations, obtained with atmospheric density corrections on 773,998 realizations, including all SOs, was equal to 14.4%. A similar characteristic calculated for 96,475 estimates on the calibration SOs was equal to 8.7%. Thus, the value of the scattering of the ballistic coefficient variations, calculated for all the SOs, decreased 1.62 times when accounting for constructed atmospheric density variations, and 1.82 times for the calibration SOs.

The presented results support the conclusion that estimations of the upper atmosphere density, obtained after density corrections, track the real changes of the density much better, than the employed GOST and NRLMSIS-00 models.

Table 1. The generalized statistics for distribution of ballistic coefficient estimates (the GOST model).

Secondary data processing mode Data covering interval All SOs Calibration SOs
Number of Kb
estimates		 SD, % Number of Kb
estimates		 SD,%
Without density correction 4 year 794906 23.4 97881 15.8
With density correction 4 year 773998 14.4 96475 8.7

Let's now consider the influence of the atmospheric density corrections on the accuracy of the orbit prediction. For the GOST model these results were obtained for two years of the overall time interval: 2000 and 2002. The 2000 interval is of interest, because the upper atmosphere was strongly perturbed during this period. The year 2002 was the quietest year from the viewpoint of intensity and frequency of disturbances of the upper atmosphere density. The orbit predictions were carried out for all the space objects that were chosen for the experiment. To obtain the comparable error statistics across all satellites and for different prediction intervals normalized error parameters were used [10]. Table 2 presents the generalized statistical characteristics for the distribution of normalized prediction errors, obtained with and without atmospheric density correction. The averaged values of the standard deviation for the prediction errors, obtained without and with the corrections of the atmospheric density, are equal to 29.2% and 16.5%, respectively, for 2000. For the calibration SOs, the appropriate SD values are 27.9% and 13.7%. Thus, on the interval of 2000 the density correction results in a reduction in the prediction errors of 1.77 times for all SOs, and by 2.03 times for the calibration SOs. For the rather quiet period of 2002 the density correction results in the accuracy increasing by 1.41 for all SOs, and by 1.78 for the calibration SOs.

The influence of applying the density corrections on the accuracy of predictions for the NRLMSIS-00 model has been estimated by comparison of the results of SO’s reentry time predictions [12]. Table 3 generalizes data characterizing the influence of density corrections to the NRLMSIS-00 model for Starshine satellites of spherical shape. It is seen from the data of Table 3 that the application of density corrections to the NRLMSIS-00 model has decreased the prediction errors for satellites of Starshine series by factors of 5.7, 3.0 and 1.6. The root-mean-square (RMS) values of reentry prediction errors were in the range from 4.9% to 8.1% before density corrections. The residual level of RMS errors after density corrections decreased to the range from 1.4% to 3.1%.

Table 2. The generalized statistics of prediction errors

Fitting and prediction process mode Covering interval All SOs Calibration SOs
Number of
predictions 		SD, % Number of
predictions 		SD,%
Without density correction 2000 652907 29.2 87274 27.9
2002 1983545 21.5 276543 20.2
With density correction 2000 652478 16.5 87533 13.7
2002 1983476 15.2 276615 11.3

Table 3. Statistics for reentry prediction errors for Starshine satellites.

SO# Number of predictions RMS for relative errors
Of reentry prediction, %		 Ratio of RMS
Without density correction With density correction
25769 91 8.1 1.4 5.7
26929 65 6.5 2.1 3.0
26996 68 4.9 3.1 1.6

Calculations, which demonstrate the impact of the density corrections on the reentry prediction accuracy, were carried out additionally for 95 chosen LEO space objects having arbitrary shapes. For the majority of the objects the prediction interval was limited to 10 days. The average value of prediction numbers for SOs of this group was equal to 31. The average value of RMS errors for the case of predictions without density corrections is equal to 9.1%. The correspondent value of RMS after density correction equals 6.9%, i.e. it decreased by 32%.
6. ESTIMATION OF TRUE BALLISTIC COEFFICIENT VALUES

For calculating the density corrections for each ith space object, especially for calibration satellites, it is necessary to know, as precisely as possible, the estimate of a ‘true’ value of the SO’s ballistic coefficient we designated as ki. The ballistic coefficient is determined in our calculations as

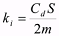         (4)

where Cd is the dimensionless coefficient of drag, S is the cross-sectional area perpendicular to satellite’s motion, and m is the mass.

The estimate of the true value of a ballistic coefficient of our calculating was determined as an average value of all the ballistic coefficient estimates for the given SO

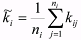         (5)

where kij denotes the jth ballistic coefficient estimate for the ith space object; n is the number of ballistic coefficient estimates obtained for the ith space object.

For verification, the true values of ballistic coefficients, estimated by us for the NRLMSIS-00 model, have been compared with the similar estimates obtained in the construction of the High Accuracy Satellite Drag Model (HASDM), and the theoretical values calculated for spherical SOs [11]. Table 4 summarizes the results of the estimations of true ballistic coefficient values that we have obtained for all 16 selected SOs. The first column gives the NORAD catalog numbers for space objects. The second and third columns present, respectively, the numbers of estimates (ni) and covering intervals, over which the estimates of true values of ballistic coefficients were obtained using the NRLMSIS-00 model. The true values of ballistic coefficient estimates (5) are presented in the fourth column. For comparison, the estimates of true values of ballistic coefficients B/2, obtained in the HASDM construction [16–19], are presented in the fifth column. These data were calculated by averaging the ballistic coefficient estimates obtained over a 30-year interval for all considered SOs, except the satellites of Starshine series. The Jañchia atmosphere model [20] has been used as the base model in the HASDM. The sixth column contains the theoretical values of the ballistic coefficients for some SOs of spherical shape calculated by formula (4). The seventh column of the table presents the relative differences, in percentage, between our estimates of true values of ballistic coefficients and estimates obtained during the HASDM construction. And the last column gives the relative differences, in percentage, between our estimates of true values of ballistic coefficients and theoretical estimates.

The data of Table 4 testify to a very good coincidence of our estimates of true ballistic coefficient values with the estimates obtained during the HASDM construction. A difference between these estimates equals only 1.3% on the average! The maximum distinction between these estimates obtained by data averaging over different time intervals and for different atmosphere models is equal to 4.3%.

It follows from the analysis of the last column data, that our estimates agree a little worse with the theoretical estimates of ballistic coefficients, which were calculated under an assumption that the aerodynamic drag coefficient Cd is equal to 2.1 for all SOs. The maximum distinction of obtained estimates of true values of ballistic coefficients from their theoretical values equals -6.8%. The average value of difference between experimental and calculated values equals -3.39%. It is also seen from these data that for the majority of SOs, the theoretical value of the ballistic coefficient is greater than the experimental one. Note also that we have calculated the theoretical values for Cd=2.1, though in reality it is recommended to let Cd=2.2 for spherical-shaped SOs. Taking these circumstances into account, one can suppose that the NRLMSIS-00 atmosphere model has a bias on the considered time interval. As a result, this model may give at 200-600 km altitudes more high values of density, on the average. The relative value of this bias can lie in the range from 3% to 8%, and, possibly, this value depends on the altitude.

Table 4. True ballistic coefficients.

SO# ni Cover interval,
days 		~ki,
m2/kg 		~B/2
, m2/kg
(HASDM)		 ki
m2/kg
(Cd=2.1)		 ~ki - ~B/2
%		 ~ki - ki
%
22 1675 1455 0.01169 0.01118 - 4.3 -
60 2068 1455 0.01133 0.01118 - 1.3 -
63 1576 1454 0.00743 0.00714 - 3.9 -
165 1708 1455 0.02663 0.02557 - 2.0 -
229 1355 980 0.02610 0.02578 - 1.2 -
2611 1611 1095 0.01157 0.01161 - -0.3 -
7337 1914 1456 0.00560 0.00560 0.00583 0 -4.1
8744 2008 1456 0.00553 0.00558 0.00583 -0.9 -5.4
12138 1779 1456 0.00561 0.00557 0.00583 0.7 -3.9
12388 1791 1445 0.00565 0.00561 0.00583 0.7 -3.2
14483 1736 1456 0.00565 0.00561 0.00583 0.7 -3.2
22875 2091 1348 0.00412 0.00404 0.00440 1.9 -6.8
23853 2076 1456 0.00423 0.00416 0.00440 1.7 -4.0
25769 197 257 0.00486 - 0.00485 - 0.2
26929 925 476 0.00771 - 0.00810 - -5.0
26996 263 130 0.00508 - 0.00500 - 1.5
7. COMPARISON OF THE GOST AND NRLMSIS-00 RESULTS

The corrections to density that we calculate from the drag data of LEO space objects are, in their essence, the errors in the used models. By this reason it is interesting to compare the statistical characteristics of these corrections obtained for various models. The results of this comparison can be useful, for example, in selecting the atmosphere model for our applications, when we have to decide, which model is better for solving some specific task. These results can also be used for estimating the a priori errors of prediction.

We obtained the density corrections for two atmosphere models, namely, the GOST and NRLMSIS-00 models, over the four-year interval. Table 5 presents the statistical characteristics (the mean values and standard deviations) of density corrections for each of these two models. These characteristics were calculated for altitudes of 200, 300, 400, 500 and 600 km. Fig. 7 gives the plots of the time history of density corrections for the 600 km altitude. Fig. 8 shows the linear regression line fitted to the errors of the GOST model as a function of altitude. In the same figure the 95% confidence interval for the regression line is plotted as well. Similar scatterplots are presented in Fig. 9 for the NRLMSIS-00 model. The analysis of these data allows one to draw the following conclusions:

  1. The levels of accuracy of the GOST and NRLMSIS-00 models are close over the analyzed interval. At the 200 km-altitude the mean errors of the models are about 10%. At the 600-km altitude they reach 22-24%. The NRLMSIS-00 model gives a slightly better accuracy at altitudes up to 300 km.
  2. To calculate the standard deviation σGOST(h) for density calculation errors, the following relation can be used for the GOST model in the altitude range from 200 to 600 km:
             (6)
    where σGOST(h) is expressed in percent, altitude h is expressed in km.
  3. To calculate the standard deviation σNRLMSIS-00(h) for density calculation errors, the following relation can be used for the NRLMSIS-00 model in the altitude range from
             (7)
    where σNRLMSIS-00(h) is expressed in percent, altitude h is expressed in km. NRLMSIS 00
  4. The density corrections for the GOST model have a slightly greater mean value, than the NRLMSIS-00 model. For the GOST model this quantity reaches several percent, whereas for the NRLMSIS-00 model it does not exceed one percent.
  5. The mean value for the GOST model depends on altitude and time.
  6. Both the amplitudes and phases of density corrections for the GOST and NRLMSIS-00 models surprisingly coincide in the interval from December 1999 to June 2001. This fact is very interesting and requires additional investigation.

Table 5. True ballistic coefficients.

Altitude, km GOST model NRLMSIS-00 model
Mean, % SD, % Mean, % SD, %
200 -3.1 12.5 -0.5 9.4
300 -1.5 12.7 -0.3 11.6
400 1.4 14.7 -0.1 15.2
500 1.7 18.0 0.0 19.5
600 3.4 22.0 0.2 24.1

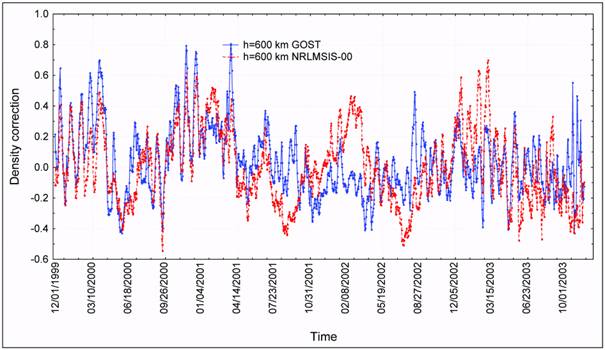Fig. 7. Comparison of density corrections constructed to the GOST and NRLMSIS-00 models for 600 km altitude.

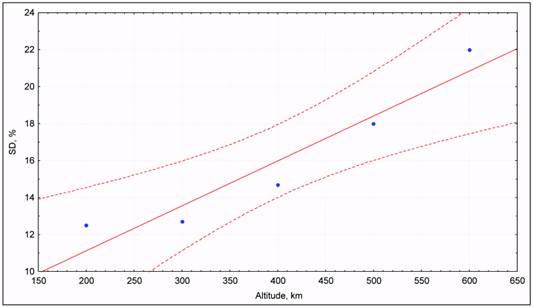Fig. 8. Altitude linear regression for errors of GOST model.

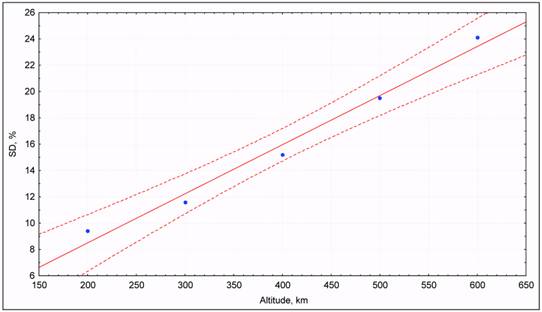Fig. 9. Altitude linear regression for errors of NRLMSIS-00 model.
8. INDIVIDUAL SO’s FEATURES

Sometimes accounting for the density corrections does not increase the orbit prediction accuracy. This can be due to the individual SO’s features of aerodynamic characteristics. Such features can be caused, for example, by the long term character of the SO’s attitude motion. Variations of a ballistic coefficient value, in some cases, for such a SO can become a main reason for motion prediction errors in the upper atmosphere.

Analysis has shown that the detection such SOs is possible by comparison of their ballistic coefficients variations, obtained without and with density corrections. The application of density corrections to the model does not eliminate the long-periodic variations in the ballistic coefficient estimates for such SOs. The common regularity in ballistic coefficient variations of these SOs is their prominent periodicity with high amplitude, whose value is commensurable with the mean value of ballistic coefficient estimates. Fig. 10 shows the plots for estimates of the ballistic coefficient, obtained with and without atmospheric density corrections, for SO #26124. For this SO the maximum estimates for ballistic coefficient differ 5.0 times from minimum ones, both before and after density corrections, and ballistic coefficient variations have a period of about 5.6 months.

The individual features in the aerodynamic characteristics behavior of SOs can be revealed by the analysis of their history of ballistic coefficients estimates obtained with density corrections. Further, these regularities can be used for forecasting the SO’s ballistic coefficient variations and their accounting in the SO’s motion prediction. The obtained results in this area [12] show that perspective methods for the solution of this task can be an auto regression and ARIMA time series analysis and forecasting methods [21–23].

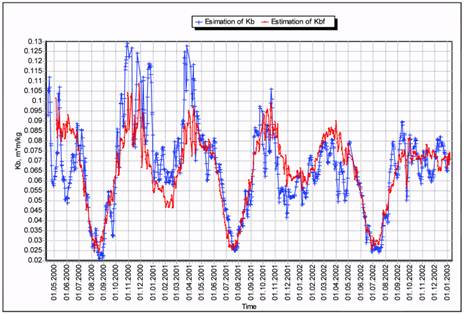Fig. 10. Ballistic coefficient variations obtained for SO#26124 without and with density corrections.
9. CONCLUSIONS

The primary source of errors in orbit determination and prediction for the LEO space objects is the inaccuracy of the upper atmosphere density models. The existing models do not represent the actual density variations with an acceptable accuracy. An effective approach for monitoring the current atmospheric density variations is based on using the available SSS drag data for the LEO space objects. This approach was first conceived more than 20 years ago and has been gradually improved since then. For the last few years our studies in this direction have been connected with the practical application of techniques, and have developed software for the construction of atmosphere density corrections using the TLE sets as input observational data. As a result, the density corrections for the GOST and NRLMSIS- 00 models were constructed with a one-day grid over a four-year interval starting in December 1999. The effectiveness of this density correction process was evaluated by comparison of the orbit determination and prediction results, obtained with and without taking into account the estimated density variations. A preliminary comparison of the obtained data with the HASDM results was made.

The applied technique and obtained results can be useful for the solution of a number of practical tasks, including:
  • increasing the orbit determination and prediction accuracy of LEO satellites at altitudes up to 600–700 km, including reentry SOs;
  • estimation of the errors of the upper atmosphere density models;
  • estimation of a priori errors for LEO satellite motion predictions;
  • finding the individual SO’s aerodynamic characteristics;
  • improvement of the upper atmosphere models.

The obtained results testify to the efficiency of the applied technique and the necessity of the continuation of work on monitoring the un-modeled variations in the atmosphere density. In this connection, the actual directions of the further work are suggested as follows:
  • extension of the density correction interval to include multiple 11-year solar cycles;
  • extension of the considered altitude range;
  • realization of monitoring of the atmosphere density variations on a regular basis;
  • increasing the time resolution of the density corrections generated;
  • detail study of the behavior of the density corrections in the vicinity of major geomagnetic storms and solar flux changes;
  • construction of the density corrections for other density models (new GOST model, Jacchia, etc.);
  • upgrading of atmosphere models using the obtained results.

Acknowledgements. The authors would like to acknowledge the representatives of the Space Surveillance community in both the USA and in Russia for supporting the US-Russian Space Surveillance Workshops in 1994, 1996, 1998, 2000, 2003 and 2005. The specific contributions of Dr. Ken Seidelmann (now at the University of Virginia), Dr. Stanislav S. Veniaminov (Scientific Research Center "Kosmos"), Dr. Felix Hoots (General Research Corporation), Dr. Alexander V. Stepanov, and Dr. Alla S. Sochilina (both from Central Astronomical Observatory at Pulkovo of the Russian Academy of Sciences) in organizing these workshops are noted. These workshops led directly to the collaboration reported in this paper. The authors would also like to acknowledge their co-workers at the MIT Lincoln Laboratory and at the Charles Stark Draper Laboratory. We are also grateful to David A. Vallado (now at Analytical Graphics, Inc.) and Dr. Chris Sabol (USAF/AFRL) for their continuing interest in this work. We are very grateful to Dr. Thomas S. Kelso (now at Analytical Graphics, Inc.) for providing the historical TLE sets using his personal WWW service [14]. The Russian authors are grateful to Andrey Bukreev (Head of the Space Informatics Analytical Systems) for his current interest in this topic.
REFERENCES
  1. Gorokhov, Yu.P., Nazarenko, A.I. “Methodical questions of construction the model of atmosphere parameters fluctuations”. Nablyudeniya Isk. Sputn. Astronomical Council of the USSR Acad. Sci., Moscow, # 80, 1982.
  2. Nazarenko, A.I. Technology of Evaluation of Atmosphere Density Variation Based on the Space Surveillance System’s Orbital Data. Proceedings of the Second US-Russian Space Surveillance Workshop, Poznan, Poland, 1996.
  3. Earth’s Upper Atmosphere. Density Model for Ballistic Support of Flights of Artificial Earth Satellites GOST 25645.115-84, Publishing House for the Standards, Moscow, 1985.
  4. Picone, J.M., Hedin, A.E., Drob, D.P., and Aikin, NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues, J. Geophys. Res., 107(A12), 1468, doi:10.1029/2002JA009430, 2002.
  5. Yurasov, Vasiliy S., Nazarenko, Andrey I., Cefola, Paul J., Alfriend Kyle T. Application of the ARIMA Model to Analyze and Forecast the Time Series of Density Corrections for NRLMSIS-00. The Sixth US- Russian Space Surveillance Workshop, St-Petersburg, August 2005.
  6. Nazarenko, A.I., Yurasov, V.S., Cefola, P.J., Proulx, R.J., Granholm, G.R. “Monitoring of variations of the upper atmosphere density”. US-European Celestial Mechanics Workshop, Poznan, Poland, 2000.
  7. Cefola, P.J., Nazarenko, A.I., Proulx, R. J., Yurasov, V.S. “Atmospheric Density Correction Using Two Line Element Sets as the Observation Data”. AAS/AIAA Astrodynamics Specialist Conference, Big Sky, Montana, August 2003, AAS 03-626.
  8. Nazarenko, A.I., Yurasov, V.S. “Atmospheric Density Correction Using Real Orbital Data”. 17th International Symposium on Space Flight Dynamics, Moscow, June 2003.
  9. Yurasov, V.S., Nazarenko, A.I., Cefola, P.J., Proulx, R. J. “Near Real Time Corrections to the Atmospheric Density Model”. Proceedings of the Fifth US/Russian Space Surveillance Workshop, St-Petersburg, September 2003.
  10. Yurasov, V.S., Nazarenko, A.I., Cefola, P.J., Alfriend, K.T. Results and Issues of Atmospheric Density Correction. 14th AAS/AIAA Space Flight Mechanics Conference, Maui, Hawaii, Feb. 2004, AAS 04-305. Published in the Journal of Astronautical Society Vol. 52, No. 3, July-September 2004.
  11. Yurasov, V.S., Nazarenko, A. I., Cefola, P. J., Alfriend, K. T. Density Corrections for the NRLMSIS-00 Atmosphere Model, AAS/AIAA Space Flight Mechanics Conference, Copper Mountain, Co. January 23-27, 2005, AAS 05-168.
  12. Yurasov, V.S., Nazarenko, A.I., Alfriend, K.T., Cefola, P.J. Reentry Time Prediction Using Atmospheric Density Corrections. Fourth European Conference on Space Debris, Darmstadt, Germany, Apr. 2005.
  13. Orbital Information Group (OIG) Web site, http://oig1.gsfc.nasa.gov [The NASA OIG web site ceased operations on 31 March 2005; similar information is now provided by a US Headquarters Air Force Space Command (HQ AFSPC) web site: http://www.space-track.org. NASA OIG users were able to access the new web site.]
  14. CelesTrak Web site, http://www.celestrak.com.
  15. SEC’s Web site, http://dawn.sec.noaa.gov.
  16. Bowman, Bruce R. True Satellite Ballistic Coefficient Determination for HASDM, AIAA/AAS Astrodynamics Specialist Conference, Monterey, California, August 2002. AIAA 2002-4887.
  17. Bowman, Bruce R., Marcos, Frank A., Kendra Michael J. A Method for Computing Accurate Daily Atmospheric Density Values from Satellite Drag Data. 14th AAS/AIAA Space Flight Mechanics Conference, Maui, Hawaii, February 8-12, 2004. AAS 04-173.
  18. Casali, Stephen J., Barker, William N., Dynamic Calibration Atmosphere (DCA) for the High Accuracy Satellite Drag Model (HASDM). AIAA/ AAS Astrodynamics Specialist Conference and Exhibit, Monterey, California, August 5-8, 2002. AIAA 2002-4888.
  19. Storz, Mark F., Bowman, Bruce R., Branson James I., Casali, Stephen J., Tobiska, Kent W. High Accuracy Satellite Drag Model, Proceedings of the Fifth US/Russian Space Surveillance Workshop, St-Petersburg, September 2003.
  20. Jacchia, L.G. New Static Models of the Thermosphere and Exosphere with Empirical Temperature Profiles. SAO Special Report No. 313, 1970.
  21. Kravchenko S.N., Nazarenko A.I. Recurrent method of the autoregression equations construction for vectorial processes. Journal of Engineering Cybernetics, Russian Academy of Sciences, #1, 1992.
  22. Nazarenko A.I., Kravchenko S.N., Tatevian S.K. The space-temporal variations of the upper atmosphere density derived from satellite drag data. Adv. Space Res. Vol. 11, #6, 1991.
  23. Box, G. E. P., & Jenkins, G. M. (1970). Time series analysis. San Francisco: Holden Day.

Ðàçìåùåí 2 äåêàáðÿ 2006.
Ãëàâíàÿ Íîâîñòè ÏóëÊÎÍ ÐÑÄÁ Îáñåðâàòîðèè Ïóáëèêàöèè About us Êîíòàêò