THE SEMIANNUAL THERMOSPHERIC DENSITY VARIATION FROM 1970 TO 2002 BETWEEN 200-1100 KM

Bruce R. Bowman

The semiannual density variation was first discovered in 1961¹. Paetzold and Zschorner observed a global density variation from analysis of satellite drag data, which showed a 6- month periodicity maximum occurring in April and October, and minimum occurring in January and July. Many authors, such as King-Hele², Cook³, and Jacchia⁴, analyzed the semiannual effect from satellite drag during the 1960s and early 1970s. They found that the semiannual variation was a worldwide effect with the times of the yearly maximum and minimum occurring independent of height. However, the semiannual period was found to be only approximate, as the times of occurrence of the minimums and maximums seemed to vary from year to year. Generally the October maximum exceeded that in April and the July minimum was deeper than that in January. None of the results showed any correlation of the semiannual variations with solar activity. Thus, the main driving mechanism for the observed variability in the semiannual variation remained a mystery. Jacchia⁴ first modeled the effect as a temperature variation. However, he soon discovered difficulties with the temperature model, and eventually modeled the semiannual variation as a density variation^5,6. He also found that the amplitude of the semiannual density variation was strongly height-dependent and variable from year to year. However, he again found no correlation of the variation with solar activity. All the previous analyses were limited to a relatively short time interval of a few years. More recent studies^7,8,9 have combined together several years of satellite drag data to analyze the semiannual variation, thus again missing the year-to-year variability. The purpose of this current study is to quantify the year-to-year variation over the last three solar cycles, and to prove or disprove the conclusion that the semiannual effect is not dependent upon solar activity.

Daily temperature corrections to the US Air Force High Accuracy Satellite Drag Model’s (HASDM)^10,11 modified Jacchia⁶ 1970 atmospheric model have been obtained on 13 satellites throughout the period 1970 through 2002. Approximately 120,000 daily temperature values were obtained using a special energy dissipation rate (EDR) method¹², where radar and optical observations are fit with special orbit perturbations. For each satellite tracked from 1970 through 2000 approximately 100,000 radar and optical observations were available for special perturbation orbit fitting. A differential orbit correction program was used to fit the observations to obtain the standard 6 Keplerian elements plus the ballistic coefficient. “True” ballistic coefficients¹³ were then used with the observed daily temperature corrections to obtain daily density values for different reference heights (average perigee heights). The daily density computation was validated³ by comparing historical daily density values computed for the last 30 years for over 30 satellites. The accuracy of the density values was determined from comparisons of geographically overlapping perigee location data, with over 8500 pairs of density values used in the comparisons. The density errors were found to be less than 4% overall, with errors on the order of 2% for values covering the latest solar maximum. The latter decrease in error is largely due to increased observation rates.

Table 1 lists all the satellites used for this study. A variety of orbit inclinations, from low to high, were used. The satellites with perigee heights below 600 km are in moderate eccentric orbits with apogee heights varying from 1500 km to over 5000 km. The majority of the satellites are spheres, which avoids the possibility of frontal area problems producing invalid drag results.

Table 1. Satellites used for the semiannual density variation study.
Table is sorted by perigee height (in bold).

NORAD	INTL	NAME	Shape	True B (m2/kg)	INCL (deg)	Apogee (km)	Perigee (km)	Start	End
6073	1972-023E	Venus Lander	Spheroid	0.00356	52.1	9800	220	1973	2002
4053	1969-064C	Intelsat	Cylinder	0.00582	30.2	5400	265	1971	2002
13985	1983-030B	Delta R/B	Cylinder	0.01851	25.3	4020	290	1984	2000
6895	1973-078C	Delta 1 R/B	Cylinder	0.01745	28.8	2320	350	1974	1995
12388	1981-033A	Cosmos 1263	Sphere	0.01121	83.0	1525	405	1982	2002
3827	1969-025E	OV1-19 R/B	Cylinder	0.02289	104.8	5450	500	1970	2002
11	1959-001A	Vanguard 2	Sphere	0.05039	32.9	3000	560	1969	2002
45	1960-007A	Transit 2A	Sphere	0.01615	66.7	975	625	1969	2002
1738	1965-093A	Explorer 30	Sphere	0.01572	59.7	850	700	1969	2002
5398	1971-067E	Rigidsphere 2	Sphere	0.06098	87.6	850	775	1972	2002
2826	1967-053A	Surcal 160	Sphere	0.19279	69.9	900	850	1969	2002
900	1964-063C	Calsphere 1	Sphere	0.24239	90.2	1050	1025	1969	2002
1520	1965-065H	Calsphere 4	Sphere	0.06994	90.1	1180	1100	1969	2002

The start and end years for the time span used in the data analysis are listed. The moderate eccentric apogee heights are shown in bold.

The semiannual variations were computed first by differencing the computed daily density values with density values obtained from the HASDM modified Jacchia atmospheric model without applying both the daily temperature corrections and Jacchia’s semiannual equations. If Jacchia’s model were perfect then the resulting differences would only contain the observed semiannual variation. This is equivalent to computing the “Density Index” D that has previously been used¹⁴ to compute the semiannual variation. Figures 1 and 2 show examples of the individual density differences obtained from the data. Also shown is the Jacchia semiannual density variation, and a Fourier series fitted to smoothed density difference values. This Fourier function is discussed in detail below. As can be observed in the two figures, there is a very large unmodeled 27-day variation in the difference values. This most likely results from Jacchia’s model inadequately modeling the 27-day solar EUV effects. Because of the very large 27-day variations in the data, it was decided to smooth the values with a 28-day moving filter. The resulting values would then produce a smoother fit with the Fourier series.

It is interesting to note how the semiannual variation changes with height and time. Figure 1 shows the variation during a year near solar maximum (2002), while Figure 2 shows the variation during a solar minimum year (1993). The semiannual amplitude is measure from the yearly minimum, normally occurring in July, to the yearly maximum, normally in October. During solar maximum, the semiannual variation can be as small as 30% at 220 km, and as high as 250% near 800 km. During solar minimum, the maximum variation near 800 km is only 70% as shown in Figure 2. Thus, there is a major difference in amplitudes of the yearly variation from solar minimum to solar maximum, unlike Jacchia’s model, which maintains constant amplitude from year to year. This is discussed in detail below.

Fig. 1. Semiannual density variation for 2002 for selected satellites. Individual points are daily density difference values. Jacchia’s model and individual satellite Fourier fit also plotted. The top and bottom set of curves have been offset in Dlog Rho (Δlog₁₀ρ) by +0.5 and –0.5 respectively for clarity.

Fig. 2. Semiannual density variation for 1993 for selected satellites. Amplitude of semiannual variation also shown as percent density changes. The top and bottom set of curves have been offset in Dlog Rho (Δlog₁₀ρ) by +0.5 and –0.5 respectively for clarity.

Initially Jacchia⁴ represented the semiannual density variations as a temperature variation. However, many difficulties arose from this that could not be explained in temperature space, so, to remove these difficulties, Jacchia eventually had to assume that the semiannual variation was not cause by temperature, but by direct density variations. From Jacchia’s analysis of 12 years of satellite drag data^5,6 he obtained the following equations. Jacchia represented the semiannual density variation in the form:

      (1)

G(t) represents the average density variation as a function of time in which the amplitude (i.e. the difference in log₁₀ density between the principal minimum in July and the principle maximum in October) is normalized to 1, and F(z) is the relation between the amplitude and the height z. Jacchia’s 1977¹⁵ Model F(z) and G(t) functions are:

      (2)

      (3)

τ is a periodic function of the fraction of the tropical year T (365.0 days) corresponding to the day of the year t.

      (4)

      (5)

Other studies⁸ used only annual and semiannual periodic terms to capture the yearly G(t) variations, although Jacchia did not believe that using only these terms was sufficient to capture the full semiannual variation.

In this study it was determined that a Fourier series could accurately represent Jacchia’s G(t) equation structure and simplify the solution of the coefficients. It was determined that a 9 coefficient series, including frequencies up to 4 cycles per year, was sufficient to capture all the variability in G(t) that had been previously observed by Jacchia and others.

It was also determined that a simplified quadratic polynomial equation in z could sufficiently capture Jacchia’s F(z) equation and not lose any fidelity in the observed F(z) values.

The resulting equations used for the initial phase of this study were:

      (6)

      (7)

      (8)

The amplitude, F(z), of the semiannual variation was determined on a year-by-year and satellite-by-satellite basis. The smoothed density difference data was fit each year for each satellite using the 9 term Fourier series (Equation (7)). The F(z) value was then computed from each fit as the difference between the minimum and maximum values.

Fig. 3. The amplitude function F(z) for three different years (1990, 1993, 2002), with semiannual amplitudes plotted for each satellite for each year. The standard deviation, ‘sig’, of the fits is shown. The constant F(z) function from Jacchia is also plotted.

Fig. 4. The fitted F(z) curves for solar minimum (1993) through solar maximum (2001). Solar min years are in blue, solar mid years are in yellow, and solar max years are in red.

Figure 3 shows the results of three different years of data, along with the plot of Jacchia’s standard 1977 F(z) equation. For each year, the
values were fit with a quadratic polynomial in height. The smoothed curves shown in Figure 3 represent the least squares quadratic fit obtained for three different years. The Δlog₁₀ρ data for all satellites are very consistent within each year, producing a standard deviation of only 0.03. The most notable item in Figure 3 is the very large difference in maximum amplitude among the years displayed. The 2002 data shows a maximum density variation of 250% near 800km, while the 1993 data shows only a 60% maximum variation. Jacchia’s F(z) function only gives a constant 130% maximum variation for all years. Figure 4 shows the quadratic fits from solar minimum year 1993 through solar maximum year 2001. The year-to-year amplitude changes are readily apparent, with the greatest differences occurring during solar maximum.

From analysis of data during the 1960s and early 1970s Jacchia found no noticeable variation in F(z) with respect to solar activity. However, this study used over 30 years of data covering three separate solar cycles, so an attempt was made to see if any correlation exists between the F(z) values and the average F_10.7 value. The observed maximum value of F(z) for each year was used for the correlation. Figure 5 shows a plot of the F(z) maximum yearly values with respect to the yearly F_10.7 average. The maximum F(z) values show an extremely high correlation with the yearly average value of F_10.7. Three years, 1988, 1993, and 2002 were rejected from the fit because their values deviated by more than 3 sigma from the fitted line shown in the figure. Some error was introduced using a yearly average of F_10.7. However, the resulting fitted sigma was 0.04 in Δlog₁₀ρ, indicating a very good fit with high correlation.

Figure 6 shows the correlation of the each year’s maximum F(z) value with height. The data shows that the height of the maximum value moves from the 600-700 km range during solar minimum to the 800-900 km range during solar maximum. The 600-700 km solar minimum range is significant in that during solar minimum the major molecular constituent above 600 km (up to 1500 km) is helium. During solar maximum the helium boundary moves up to about 1500 km, above which it becomes the dominant constituent. This fact will be emphasized in a later section describing when the semiannual variation disappears above 600 km during solar minimum.

To obtain a global fit, covering all years and all heights, all F(z) values for all satellites and all years were fitted to obtained the F(z) Global Model using the following equation:

      (9)

where z = (perigee height/1000) (km), and F_10.7 is the yearly average of F_10.7.

From the linear correlation of the F(z) yearly maximum with respect to F_10.7 the global equation needed to include only an additional linear function of F_10.7 along with the quadratic z functionality. A sigma of 0.048 in Δlog₁₀ρ was obtained using a 3-sigma rejection to eliminate outlier values. The yearly maximum global F(z) values were then computed from Equation (9). Figure 7 shows the observed yearly maximum F(z) values and the fitted F(z) Global Model maximum values plotted as a function of date. Also shown are the 90-day average F_10.7 values. The strong correlation of the yearly maximum F(z) values with F_10.7 is readily apparent. Also apparent are the occasional odd years (i.e. 1988, 1993, and 2002) that appear to occur less than 10% of the time. In conclusion, the high variability found in the amplitude of the semiannual variation has been discovered to indeed be highly correlated with solar EUV activity.

Fig. 5. The maximum F(z) value for each year plotted as a function of the yearly average F_10.7. The standard deviation, ‘sig’, of the fit is shown, as well as the Jacchia value. The data from the years 1990 through 2000 is highlighted (1990s Data).

Fig. 6. The maximum F(z) value for each year plotted as a function of the height of the maximum value. The data from the years 1990 through 2000 is highlighted (1990s Data).

Fig. 7. The observed maximum F(z) value for each year plotted by year. Also shown are the computed maximum F(z) values using the Global Model. The 90-day F_10.7 average, F10B, is displayed, along with Jacchia’s constant maximum amplitude value.

The G(t) function, as previously discussed, consists of a Fourier series with 9 coefficients. The 28-day smoothed density difference data for each satellite was fitted with the Fourier series for each year. The density difference data is the accurate observed daily density values minus the Jacchia values without Jacchia’s semiannual variation. The G(t) function was then obtained by normalizing to a value of 1 the difference between the minimum and maximum values for the year. The F(z) value for each satellite by year was used for the normalization. Figure 8 shows the results obtained for the year 1990 for the majority of the satellites. Note the tight consistency of the curves for all heights, covering over 800 km in altitude. A yearly G(t) function was then fit using the data for all the satellites for each year. Figure 8 also shows the yearly G(t) value, with a standard deviation of 0.11 in Δlog₁₀ρ. A small sigma was obtained for every year’s fit, especially during solar maximum years. Figure 9 shows the yearly G(t) fits for 1999 through 2001. It is readily apparent that the series changes dramatically from year to year. During solar maximum the July minimum date can vary by as much as 80 days. Figure 10 demonstrates the yearly G(t) variability occurring during solar maximum and solar minimum. The variability is especially large for defining the time of the July minimum during solar maximum, while the solar minimum times show much more consistency from year to year.

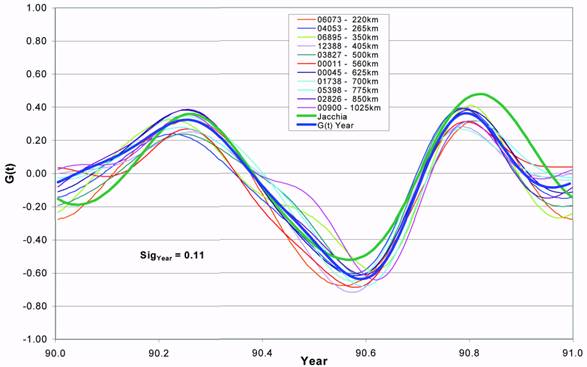Fig. 8. The individual satellite G(t) fits are plotted for 1990. The Jacchia model and yearly fit model are also shown. The standard deviation, ‘Sig_Year‘, for the G(t) Year Model is displayed.

Fig. 9. The individual satellite fits for 3 different years is shown. The Year G(t) Model is highlighted. Each set of curves for 1999 and 2001 has been offset by +1.00 and –1.00 respectively in G(t) for clarity.

Fig. 10. The yearly G(t) fitted curves for different years are shown for solar minimum and solar maximum conditions. The Solar Min set of curves is offset by –1.00 in G(t) for clarity. The average July minimum date with standard deviation is shown.

In an attempt to explain the variability of the July minimum date a 28-day average of F_10.7 was computed. Figure 11 shows the plots of the 28-day average, the 90-day F_10.7 average, and the Year Model values, all for the year 2000. The 28-day and 90-day averages are given for the end point of each interval. The date of a maximum difference value was determined for each year. The maximum difference value is the maximum value of the 28- day average above the 90-day average value occurring during the March (Day 60) through July (Day 212) time period, always prior to the July minimum date. If there are two or more maximums of near equal value then the closest one to the July minimum date is selected. Figure 12 shows a plot of the date of this F_10.7 maximum difference verses the date of the July minimum for the same year. The correlation is striking. If the date of the maximum difference occurs early in the March to July time period then the July minimum date occurs as early as mid June. If, however, the maximum difference occurs much later in the time period then the July minimum is delayed, sometimes to the point of occurring as late as the end of August. It is interesting to note that other maximum differences do not appear to shift the date of the October semiannual maximum, and they have only a small effect on shifting the date of the semiannual April maximum. Apparently, the solar EUV is driving the phase shifts of the semiannual July minimum as well as driving the previously shown amplitude variations of the overall semiannual variation. This again demonstrates the need for a yearly variable Fourier function representing the different solar conditions that occur each year.

Fig. 11. Plots of the 28-day and 90-day F_10.7 running averages (values are for the end point of the interval). The Year G(t) Model values are also plotted, all for the year 2000.

Fig. 12. The correlation of the July minimum date with the date of the F_10.7 maximum difference value. The equation for the July minimum date is given as a time lag of the date of the F_10.7 maximum difference date. Also shown is the standard deviation, ‘Sigma’, of the linear fit.

Fig. 13. The G(t) curves for different solar activity as computed from the G(t) Global Model is shown. The standard deviation, ‘Sig’, of the global fit is displayed.

A global G(t) function was then obtained using all satellite data for all years. Since the yearly G(t) functions demonstrated a dependence on solar activity it was decided to expand the series as a function of the 90-day average F_10.7. Since the F(z) function showed only a linear correlation with F_10.7 the following equation was adopted for the global G(t) function:

      (10)

Figure 13 is a plot of the above global G(t) equation as fitted with all the satellite data. Jacchia’s equation for G(t) is also shown. The standard deviation of the global fit was 0.16 Δlog₁₀ρ. It is interesting to note that the solar minimum and solar maximum plots are significantly different except near the October maximum, which appears to have only a slight phase shift. The April maximum variation is much larger in amplitude, though not in phase. Jacchia’s function overestimates the October maximum for all solar activity, and only correctly estimates the April maximum during average solar activity. The curves once again demonstrate the need for solar activity to be included in the G(t) function.

An interesting phenomenon occurs only during solar minimum (F_10.7 < 80) at altitudes above 600 km. The following can be observed:

1. The semiannual variation almost disappears. The minimums are gone, and only a hint of the October maximum is visible.
2. The July minimum turns into a maximum as the altitude increases.
3. The July “minimum-maximum” shifts from occurring in mid July at 600-700 km to occurring in late August at 1100 km.
4. The smoothly varying day-to-day variations turn into very scattered variations at the higher altitudes, but only during the July to September time period.

Figures 14 through 16, for solar minimum years 1975, 1986, and 1996, show the occurrence of the above phenomenon. The semiannual variation has flattened out to where there is only a hint of the October minimum. This is not the case during solar maximum (Figures 1 and 2) where there is a significant semiannual variation at all altitudes. However, the unmodeled 27-day variation in the density differences is still observable in Figures 14 through 16, as it is at solar maximum, with the largest variations occurring in the 600 to 700 km altitude range, and decreasing with altitude. The really interesting phenomenon that is readily apparent is that the previously observed July minimum changes into a maximum value as the altitude increases. At 600 to 700 km there is a hint that the July minimum is turning into a maximum value, while at the 1100 km altitude a definite yearly July maximum is observed. This maximum value appears to occur later and later in the year as the altitude increases. Figure 17 shows a plot of the occurrence of the “July” minimum-maximum point with altitude. Even with a lot of scatter in the plot it is obvious that the date of the occurrence gets later with altitude. Below 600 km the July minimum is occurring around mid-July (year day 190). As the altitude increases from 700 km to 1100 km the date increases from late July to late August (year day 240). Still another interesting effect occurring during this time is the large day-to-day scatter of density residuals. This occurs with all the satellites above 600 km, but only during the July to late August time period. Figures 14 through 16 show the daily density differences are smooth at all altitudes for the rest of the year except for this short time period. The amount of scatter increases with altitude, with almost none at or below 700 km. Satellite 00011 at 560 km showed none of the higher altitude variations in the amplitude or scatter from the normally observed semiannual variation during solar maximum. It is as if the atmosphere does not hold any day-to-day consistency but changes rapidly with no time correlation. Since this is observable with all satellites, and only during this July to late August time period, it cannot be attributed to orbit fitting problems. During solar minimum the atmosphere is dominated by helium above 600 km (up to 1500 km), while during solar maximum helium starts becoming dominant only above 1500 km. If the theory by Fuller- Rowell¹⁶ is corrected (refer to the discussion below) then the atmosphere is very compressed during the summer solstice, especially during solar minimum, which may have the effect of replacing helium with hydrogen as the main constituent above 700 km during these time periods. What is then being observed is the ineffectiveness of either helium or hydrogen to retain any day-to-day correlation with solar EUV variability.

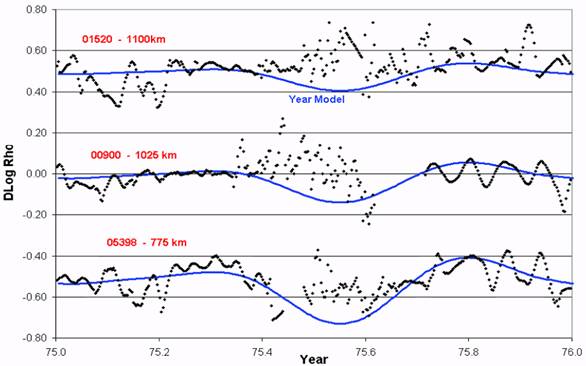Fig. 14. Plot of Dlog Rho (Δlog₁₀ρ) for high altitude satellites during solar minimum year 1975. The Year Model is also shown. The data and curves for 01520 and 05398 have been offset by +0.50 and –0.50 respectively for clarity.

Fig. 15. Plot of Dlog Rho (Δlog₁₀ρ) for high altitude satellites during solar minimum year 1986. The Year Model is also shown. The data and curves for 01520 and 00045 have been offset by +0.50 and –0.50 respectively for clarity.

Fig. 16. Plot of Dlog Rho (Δlog₁₀ρ) for high altitude satellites during solar minimum year 1996. The Year Model is also shown. The data and curves for 01520 and 01738 have been offset by +0.50 and –0.50 respectively for clarity.

Fig. 17. The July minimum/maximum date is plotted for all satellites during solar minimum times. The years 1976 and 1986 are highlighted.

It is interesting to interpret the variation in the magnitude of the semi-annual variation with solar activity in the context of the “thermospheric spoon” theory suggested by Fuller- Rowell¹⁶. The “thermospheric spoon” explanation of the semi-annual variation suggests that the global-scale, interhemispheric circulation at solstice acts like a huge turbulent eddy in mixing the major thermospheric species. The effect causes less diffusive separation of species at solstice, mixes the atomic and molecular neutral atmosphere species, leading to an increase in mean mass at a given altitude. The increased mean mass at solstice reduces the pressure scale height. The “compression” of the atmosphere leads to a reduction in the mass density at a given height at solstice. In contrast, at equinox, the global circulation is more symmetric and weaker. The weaker circulation no longer mixes the atmosphere, allowing the lighter species to separate out under diffusive equilibrium. The atmosphere expands leading to an increase in mass density at a given altitude at equinox. This theory can explain the semi- annual variation in mass density.

Tim Fuller-Rowell¹⁷ states “the theory also suggests that the strength of the semi-annual variation is dependent on the vigor of the seasonal circulation cell. The increase in the semiannual variation seen in the drag data therefore implies that the global circulation is stronger at high solar activity. This is a reasonable assumption given that solar heating and pressure gradients will be greater at solar maximum”. It remains to be seen if theoretical physically-based models support this explanation.

An error analysis was conducted to determine the errors of the Year, Global, and Jacchia models previously described. The “Satellite Fit” Model was used for determining the semiannual variation error. This model is for each individual satellite for each year fitting a 9 coefficient Fourier series to the 28-day smoothed density difference values. The fits were done on a satellite-by-satellite basis for every year of available data. These fits should represent the “true” year-to-year semiannual variation experienced by each satellite. The Year Model is the year-to-year coefficients determined from all the satellites for the given year. The Global Model is the one set of coefficients representing the semiannual variation for all years and all altitudes. The density error from the contribution of the semiannual variation error was obtained by differencing the Year, Global, and Jacchia models from the “Satellite Fit” values. The total (semiannual, EUV, diurnal, etc.) error for each model was then obtained by differencing the original density difference data from the model predictions. The difference between the total and semiannual errors was attributed to the unmodeled EUV, diurnal, and other density variation errors.

Figure 18 shows the semiannual density errors from the Year, Global, and Jacchia models for solar minimum years. The Jacchia model, as expected, is the worse model, while the Year Model is the best. The Global model appears to be modeling the semiannual variation almost as well as the Year Model. From previous discussions the Global Model did capture the yearly G(t) function much better at solar minimum than at solar maximum. Figure 19 shows the semiannual density errors for all years combined. As expected the Global Model does not show much of an improvement over the Jacchia model because of the much larger year-to-year G(t) variations found for years with moderate to high solar activity. However, the much lower 5-10% standard deviation for the Year Model clearly demonstrates that a year-to-year model approach will provide a very significant reduction in the current unmodeled semiannual density errors.

Finally, the variances of the semiannual variations are displayed in Figures 20 and 21. The plots show that for the Jacchia model the unmodeled semiannual variations contribute to the error budget as much as the remaining unmodeled variations from EUV, diurnal, etc. effects. Figure 21 then shows that using the Year Model greatly reduces the contribution of the unmodeled semiannual variations, to the point that almost all of the remaining error can be attributed to other error sources (EUV, diurnal, etc.).

Fig. 18. The different model density errors (percent density) are shown for all data during solar minimum periods.

Fig. 19. The different model density errors (percent density) are shown for all data for all solar activity.

Fig. 20. The variance (times 1000) in Dlog Rho (Δlog₁₀ρ) is shown for the semiannual errors and the remaining errors (EUV, diurnal, etc.) in the Jacchia Model.

Fig. 21. The variance (times 1000) in Dlog Rho (Δlog₁₀ρ) is shown for the semiannual errors and the remaining errors (EUV, diurnal, etc.) in the Semiannual Year Model.

The following results concerning the semiannual variation have been obtained from the current study:

1. The semiannual effect is worldwide, and within each year the maximum and minimum occur at the same date regardless of latitude or height (with the exception of very high altitudes during solar minimum).
2. The semiannual variation, measured at the height of maximum amplitude variation, can vary from as little as 60% during solar minimum to over 250% during solar maximum.
3. The yearly amplitude of the semiannual variation is highly correlated with solar activity.
4. The maximum yearly amplitude occurs at an altitude of 600-700 km during solar minimum, increasing to a height of 800-900 km during solar maximum.
5. During solar maximum the April maximum is slightly greater than the October maximum, while the reverse is true during solar minimum.
6. The July minimum/maximum date can vary by as much as 80 days, especially during solar maximum.
7. The average July minimum shifts from mid-July during solar minimum to early August during solar maximum.
8. During solar minimum the semiannual variation almost disappears at altitudes above 600 km, and the July minimum/maximum date increases in time with increasing altitude.

Final general conclusions are:

1. Accurate yearly semiannual variations have been obtained for the period 1970 through 2002.
2. Model density errors of over 100% are possible if the semiannual variation is not modeled on a yearly basis.
3. Accurate satellite drag analysis must account for these yearly variations inorder to correlate other density variations with solar effects.

Acknowledgments. This author would like to thank Mark Storz (USAF/AFSPC) for his insight and valuable contributions toward the theoretical development of the EDR method. The author also thanks Tim Fuller-Rowell (NOAA/SEC) for his useful discussions and suggestions on the semiannual density variation theory, and Robin Thurston (USAF/AFSPC) and Bill Schick (Omitron, Inc.) for supplying the USAF Space Surveillance Network satellite observations.

1. Paetzold, H.K., and Zschorner, H., “The Structure of the Upper Atmosphere and its Variations after Satellite Observations,” Space Research II, 958, North-Holland Publ. Co., Amsterdam, 1961.
2. King-Hele, D.G., and Hingston, J., “Air Density at Heights Near 190 km in 1966-7 from the Orbit of Secor 6,” Planet. Space Sci., 16, 675, 1968.
3. Cook, G.E., “The Semi-Annual Variation in the Upper Atmosphere: A Review,” Ann. Geophys., t.25, fasc.2, 451, 1969.
4. Jacchia, L.G., “Density Variations in the Heterosphere,” Annales de Geophysique, 22, 75, 1966.
5. Jacchia, L.G., “Semiannual Variation in the Heterosphere: A Reappraisal,” J. Geophys. Res., 76, 4602, 1971.
6. Jacchia, L.G., Revised Static Models of the Thermosphere and Exosphere with Empirical Temperature Profiles, Smithson. Astrophys. Special Report 332, 1971.
7. Boulton, W.J., “The Semi-Annual Variation in Air Density from June 1974 until September 1977 from the Analysis of the Orbit of Intercosmos 10 Rocket (1973-82B),” Planet. Space Sci., 35, 1127, 1987.
8. Sehnal, L., etc., “The Semi-Annual Thermospheric Density Variation Between 200-560 km,” Bull. Astron. Inst. Czechosl., 39, 209, 1988.
9. Tawadrous, M.Y., “Comparison of Observed and Modelled Semi-Annual Thermospheric Density Variations,” Bull. Astron. Inst. Czechosl., 40, 28, 1989.
10. Storz, M.F., etc., “High Accuracy Satellite Drag Model (HASDM),” AIAA 2002-4886, AIAA/AAS Astrodynamics Specialist Conference, Monterey, Ca, August, 2002.
11. Bowman, B.R., Storz, M.F., “Time Series Analysis of HASDM Thermospheric Temperature and Density Corrections,” AIAA 2002-4890, AIAA/AAS Astrodynamics Specialist Conference, Monterey, Ca, August, 2002.
12. Bowman, B.R., etc., “A Method for Computing Accurate Daily Atmospheric Density Values from Satellite Drag Data,” AAS 2004-179, AAS/AIAA Spaceflight Mechanics Meeting, Maui, Hi, February, 2004.
13. Bowman, B.R., “True Satellite Ballistic Coefficient Determination for HASDM,” AIAA 2002-4887, AIAA/AAS Astrodynamics Specialist Conference, Monterey, Ca, August, 2002.
14. Walker, D.M., “Variations in Air Density from January 1972 to April 1975 at Heights Near 200 km,” Planet. Space Sci., 26, 291, 1978.
15. Jacchia, L.G., Thermospheric Temperature, Density, and Composition: New Models, Smithson. Astrophys. Special Report 375, 1977.
16. Fuller-Rowell, T.J., “The ‘thermospheric spoon’: A mechanism for the semiannual density variation,” J. Geophys. Res., 103, 3951, 1998.
17. Fuller-Rowell, T.J., private communication.

Размещен 29 ноября 2006.