ON THE THEORY AND SOME SPECIFIC METHODS FOR SEARCHING FOR SPACE OBJECTS BY USE OF ROUGH ORBITAL INFORMATIONS. Veniaminov, V. Zavaliy, Yu. Tretyakov, V. Pyrin, V. LapukhinScientific Research Center "Kosmos", Moscow
At different conferences, symposia, and workshops the topics on positional observations of
space objects (SO) are usually concerned with two marginal categories only – the survey and
the tasked observations. The same situation took place at the 4th European Conference on
Space Debris held in Darmstadt, April this year.
The traditional approach in the first case means the consecutive scanning of some fixed
space area and detecting everything one can find there, the signal energy of a moving SO
being smeared on the receiver which does not help the acquisition of a weak signal, if so.
Besides, this strategy has two more disadvantages. These are mistakes of the 1st and 2nd kind – that is the availability of "slits" in the search plan through which the search for SO can
“come down”, and the significant redundancy of the search plan elements overlapping in
terms of what is necessary and sufficient.
All this implies unreliability of detecting SO and non-economical expense of the sensor
resources, especially when there is the task of detecting given specific SO.
The second case is the second extreme. It needs very accurate ephemerides. But what if
there are only rough ephemerides?
At the same time, between these marginal cases there exists one practically very
important type of the search situation, namely, the case when one needs to detect the specific
SO by use of a somewhat rough a priori orbital information. Such a search situation arises in
space surveillance practice, for instance, when the initial information on the search for SO is
available: the data on the time and place of the launch; the designed orbital data; the statistical
orbital data on a specific class of SOs; some estimates of the orbital parameters by rough
radar or optical measurements; some coverage information on the SO orbit; some information
on the maneuver or the orbital correction; the information on the orbital structure of a
constellation; and so on, and so on.
When we face the search situation of this type it is inexpedient to address the traditional
scanning strategy because of its unreliability and inefficiency for this kind of tasks. The
second approach mentioned fails because of lack of accurate orbital data.
By the way, mathematically, neither the first, nor the second category of the task is
interesting. Every task in its general setting has two trivial extremes in which it degenerates
mathematically: 1) when all the parameters are absolutely unknown, and 2) when the values
of all parameters are given. The task is mathematically interesting if only some parameters of
the full set are known or their values are roughly given.
Given the rough a priori orbital information, the search problem has some mathematical
intrigue. It is clear that if one disposes only of the rough orbital information, one should pay
some additional expense of the sensor resource for detecting the SO. But one should find the
solution to make this additional expenditure minimum.
The difficulties in getting the optimum solution arise from the necessary condition of
decomposing the continuously drifting and topologically deforming real SO current position
uncertainty domain into the search plan elements rather than into some fixed space area (as in
the simple scanning case).
Still more complication of the task originates from the fact that this 3-dimensional
domain (for instance, the uncertainty ellipsoid) is projected onto the picture plane of the
sensor used (also, by the by, drifting and deforming). As a result the structure and the mutual
position of the already inspected elements and the ones still to be inspected becomes
topologically very complex (see Fig. 1).
If at time-moment t0 one “cuts” the uncertainty ellipsoid projection into the search plan
elements in conformity with the size and form of the sensor field of view, then in some time
at time-moment t1 the full picture will nonlinearly change. The element A inspected at time-
moment t0 will partially “come crawling” across the neighboring element B still to be
inspected at time-moment t1, and vice versa.
This occurs because a point of the uncertainty domain projection at time-moment t0 transforms to a set (rather than a point) of the uncertainty domain projection at time-moment
t1.
For the constructive analysis and creating the real search plans with due regard for all
considered processes, a special search theory was developed [1, 2, 3] based on the so called
search plan equivalence principle [4, 5].
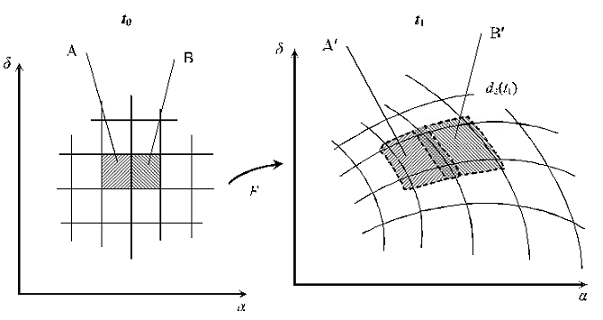 Fig. 1. The peculiarity of the temporal error transformation when projecting from the real
uncertainty domain onto the sensor picture plane.
In terms of this theory the search problem constructively comes to choosing a sequence
of conditional ephemerides and related conditional velocities of the SO's supposed motion.
This sequence is to be optimum with respect to the adopted efficiency criterion under the
restrictions laid by technical capabilities of the sensor used.
This set of conditional ephemerides and velocities (so called the generalized
ephemerides [6]) should completely cover not only the area of space, but also the
continuously drifting and topologically deforming SO's current position uncertainty domain.
Besides, this sequence (the search plan) should be the most economical one.
Eventually, after realization of this plan the entire complex of necessary favorable
conditions for correctly targeting the sensor, and keeping this direction for concentrating and
accumulating the wanted intelligence signal energy in one point of the receiver, must be
provided in one and only one case – that is for only one generalized (conditional) ephemeris
of the set. And that will do for solving our problem. All other conditional ephemerides area waste, but the necessary and minimum waste, the necessary and minimum payment for the
roughness of the a priori information about the search for SO.
Significant simplification of the task and related transformations, and reduction of
degrees of freedom can be achieved in the following, practically important cases: the search
for a lost SO; the search for a SO for which there are no measurements for a long time; the
search for a SO moving in a highly elliptical orbit after its detection by a radar in its perigee
zone; the search for a SO by a very narrow-angled facility. In these and many other cases one
may neglect all the errors but those along the track. This circumstance crucially reduces the
problem dimension in terms of the equivalence principle.
Such cases form an important niche in the Space Surveillance practice. For such cases
some search programs were developed in terms of the theory above, which were implemented
at some sites, for example, at the “Okno” site in Tajikistan. They realize the discrete search
optimum plans by the argument of latitude u. Two of them are the programs beginning from
the edge of the search area in different directions. The third one begins the inspection of the
search area from its calculated center. One can find more details in [7].
All the programs were tested together with the traditional approach (the consecutive
scanning of the fixed space area). The comparative results are given in the Table 1 where 1 is
the search program beginning from the edge of the search area in direction of the SO motion;
2, the search program beginning from the edge of the search area counter the direction of the
SO motion; 3, the search program beginning from the calculated center of the search area; 4,
the traditional method; Δts, the real duration of the search; CO, the 12-hour circular orbit;
HEO, a highly elliptical orbit.
Due to results of the work of programs the average economy of the facility resource is
about
0.4 TtrN,
where Ttr is a standard resource spent by the traditional method for detecting one SO; N, full
number of the searches for SOs in the group. One can see from the Table that in 4 cases out of
10 the SO could not detected by use of the traditional method.
One more important effect of using the above search technology is the possibility of
detecting small and weakly-contrasting space objects.
Table 1. Results of testing the traditional and proposed search methods
REFERENCES
Размещен 29 ноября 2006.
|