A STUDY OF THE SURFACE ENVELOPING THE TRAJECTORY FAMILY OF PARTICLES ISOTROPICALLY EJECTED BY A SATELLITE EXPLOSION WITH ACCOUNT FOR THE ORBIT NODE AND PERICENTER MOTIONSK. V. Kholshevnikov, S. A. OrlovAstronomical Institute of St.Petersburg University, St.Petersburg,
Petrodvoretz, Universitetsky ave. 28, 198504 RUSSIA
1. INTRODUCTIONAn explosion of an artificial satellite leads to the ejection of a mass of fragmentary particles
into the cosmic space. Typical velocities of the ejecta are of the order of one km/s or less, so
they remain on geocentric orbits T close to the supposedly circular orbit of the satellite. The
emerged swarm fills out a domain D swept by family {T}. We are interested in studying the
structure of the domain D, corresponding to the largest possible family {T}. It leads to an
assumption of the ejecta in all directions. Now let’s imagine that we observe an isotropic
ejection with all possible velocities smaller than the absolute value b.
Due to the inequality of orbital periods, the fragments will densely fill up the domain
D'. To find its boundary S', it is sufficient to suppose the velocities to be equal to b. So, D' represents a dust complex appearing a few days after the explosion.
 Fig. 1. View of S', c = 0.3
We have analytically obtained the parametric equations of the boundary S', its
properties having been examined in our previous paper [1]. Topologically, S' is a torus with
one conic point and one rectilinear constriction (see Fig. 1). In few months D' scatters due to
the motion of the nodes and pericenters of particle orbits in the gravitation field of an oblate central planet, which yields the axisymmetric solid D with the boundary ^S. Topologically, D is a torus.
Here we have obtained the parametric equations of ^S and examined its properties for the case where the orbit of the exploded satellite lies in the equatorial plane of the central planet.
2. PROPERTIES OF SSimilar to [1], we use the methods of the mathematical theory of catastrophes. The boundary ^S of D is the set of singular points of the mapping {T} → R3. Obviously, it is a body of
revolution and topologically occurs to be a torus. Hence, it is sufficient to examine its section
S by the plane xz.
The mathematical formalism, while obtaining the parametric equations of S, is rather cumbersome, so that we confine ourselves to giving the results.
The curve S is symmetric with respect to the x-axis. It consists of the convex oval S0 with two additional curvilinear triangles. These triangles are so small that they may be neglected (see Figs. 2 and 3).
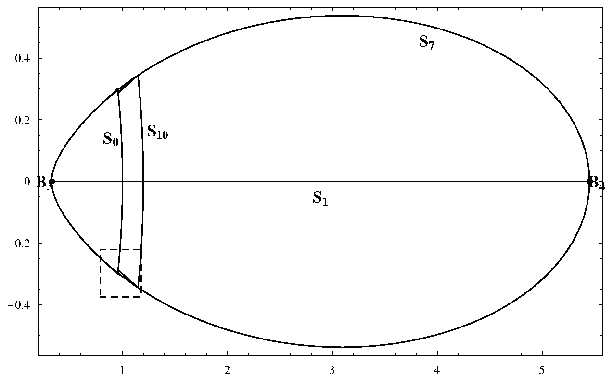 Fig. 1. View of S, c = 0.3
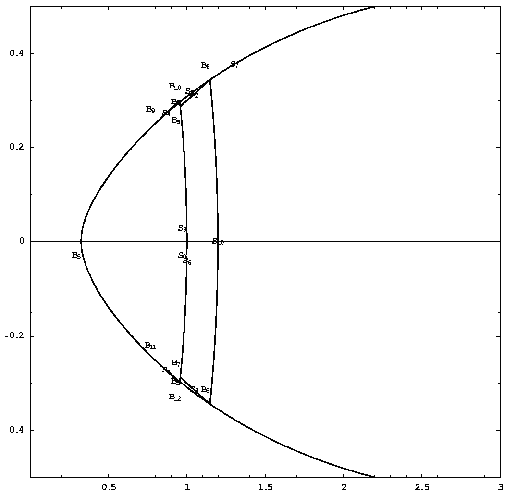 Fig. 1. View of part of S, c = 0.3
The parametric equations of S0 are
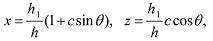 with c = b expressed in units of the circular velocity of the satellite,
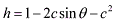  The equations are not very complicated. We can easily examine their properties and
find the following properties of S0.
The curve S0 is closed, bounded and symmetric with respect to the x-axis. The curve S0
is analytic (regular) without singular points. The curvature of S0 is negative, hence the curve
S0 is convex.
The family {S0 (c)} represents the family of embedded ovals tending to a point as c → 0. If c → 0, then S to S0 and S0 tends to an ellipse with the 1:4 axis-ratio.
3. CONCLUSIONSWe see that the boundary S of the section of D by the plane xz is an oval. If c is large, the oval
is elongated backwards from the planet. If c is small, the oval is symmetrical representing the
ellipse with the 1:4 axis-ratio.
REFERENCES
Размещен 30 ноября 2006.
|