ON ORBITAL EVOLUTION OF EXPLOSION FRAGMENTS
A. Sochilina1, R. Kiladze2, K. Grigoriev1, I. Molotov1, A. Vershkov1
1 Central Astronomical Observatory, Pulkovo road 65/1, 196140 St.-Petersburg, Russia
2 Abastumani Astrophysical Observatory, 383762,Observatory, Abastumani, Georgia
Abstract
The dynamic explosion model and its use for the investigation of geostationary object breakups are considered. It is assumed that the fragment velocity directions have a spherically symmetrical distribution. The initial fragment orbits are determined under the condition that their distances from the Earth's center are equal and the increments of their velocities differ because of their directions. At the moment of breakups the fragment orbits and the orbit of the exploded object intersect in one point of space. The study of the long-term evolution of the intersection points allowed to discover the compact distributions of these points along the orbit of the exploded object. Observations of the vicinity of such point of accumulations, which fragments have to intersect, help the search for the fragments. The method has been tested for orbital analysis of observed explosions and applied to objects, which had a sharp change in their drift rate. The results of these investigations will be presented.
INTRODUCTION
The number of geostationary objects observed by optical means is more than 900. A large number of unobserved small objects is moving in the geostationary orbit (GEO) and its vicinity eternally. An important source of space debris in GEO are explosions of geostationary objects (GS) (Jehn, 1997).
In the geostationary ring several objects have been discovered, which sharply changed their rates of drifts in the limits (0.15-1.0) °/day. Four objects have observable fragments, which permit with confidence to calculate the moments of their possible explosions. The subject of this paper is the long-term orbital evolution of fragments and their search. The time of breakup of all suspected objects have also been calculated. Today ten such objects are known. Among them there are 2 Ekrans and 8 Transtages. It is possible that the real number of explosions in GEO is more than 10.
DETERMINATION OF FRAGMENT ORBITS
Based on the formulae of the paper (Sochilina et al., 2000), new expressions have been derived, which permit to determine after the explosion of GS the direction of its fragment motion if their orbital elements are known.
It has to be noted that GS after explosion can be considered as a fragment, too. The parameters characterizing the magnitude of ΔV and the direction of V are calculated by the following formulae:
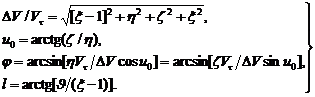
(1)
where
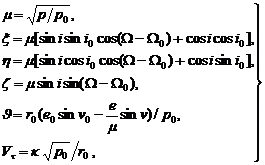
(2)
where u = v + ω, v is the true anomaly of fragment, ω - argument of perigee, e - eccentricity, a - semi-major axis, p - orbital parameter, Vτ - tangential velocity, κ - Gauss constant. The orbital elements of GS are denoted by the index "0".
Let's take a system of coordinates, in which the x axis is pointing to the vernal equinox point of date and the plane of the equator is taken as the basic plane. The position and motion of GS at the epoch T0 is determined by the position vector r0 and velocity V0. We assume, that at the moment of explosion, all fragments receive the increase of velocity ΔV, which is in the limits of 1 - 250 m/s, depending on the fragment mass; the longitude l is an angle, counted from the direction of the tangential velocity Vτ from 0° to 360°, the angle φ is counted from the plane of satellite's orbit in the limits of 90°.
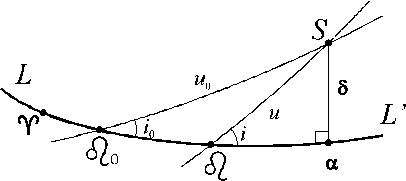
Fig. 1. The definition of the intersection place of orbits.
In Figure 1 the arc LL' corresponds to the celestial equator. The arcs Ω0S and ΩS are the projections of the orbits of GS and a fragment on the celestial sphere, S is the point of their intersection. Ω0, i0, u0 Ω, i, u denote the longitudes of nodes, inclinations of orbits and arguments of latitude of GS and fragment, accordingly. The equatorial coordinates α and δ of the intersection point S are determined from the rectangular spherical triangles ΩS and Ω0S (Figure 1) from the following equations:
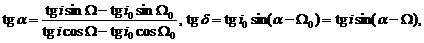
(3)
The time of the explosion is computed from the coincidence of the satellite coordinates determined with both orbital systems. The mean error of discrepancy depends on the accuracy of the used elements. For Two-Line-Elements (TLE) the error may be 5 - 10 km. In case of absence of the orbital elements during a long time (several years) the error may be larger.
In Table 1 the orbital elements of objects which may have exploded are given for the epoch of each event. The main characteristic of an explosion is a sharp change of the rate of drift, the value of which is given in the last column. These changes are in the limits of 0.1 - 1°.
For GS 76023F we did not have the orbital elements before the possible explosion, therefore the moment of explosion was calculated from the position coincidence of the object and its fragment - GS 76023J.
Table 1. Orbital elements of 10 satellites before and after possible explosion
| NN |
T0 (MJD) |
e |
i |
Ω |
ω |
λ |
dλ/dt (°/day) |
Δdλ/dt (°/day) |
| 66053J |
47071.688587 |
.010312040 |
11.°5253 |
9.°4976 |
281.°7312 |
288.°3453 |
22.°53757 |
0.°67682 |
| |
03/10/1987 |
.016240500 |
11.5321 |
9.5757 |
281.2806 |
288.9544 |
23.21439 |
|
| 67066G |
49397.408163 |
.005317158 |
11.6745 |
25.3957 |
25.8977 |
6.2241 |
32.02443 |
-0.93796 |
| |
14/02/1994 |
.008095644 |
11.6578 |
25.4061 |
5.6721 |
6.6536 |
31.08647 |
|
| 68081E |
48673.397616 |
.008544623 |
11.9100 |
21.7275 |
76.5843 |
196.7101 |
4.27995 |
0.20669 |
| |
21/02/1992 |
.008861994 |
11.9100 |
21.7541 |
71.3055 |
196.8043 |
4.48664 |
|
| 73040B |
44671.200700 |
.004358301 |
5.8669 |
62.8461 |
19.1543 |
145.2013 |
-2.32077 |
-0.21648 |
| |
08/03/1981 |
.002713236 |
5.8728 |
62.8123 |
328.2317 |
144.8817 |
-2.53725 |
|
| 73100D |
48718.887352 |
.027537580 |
13.3263 |
45.5479 |
165.4079 |
215.9878 |
-18.79458 |
-0.19387 |
| |
06/04/1992 |
.026786840 |
13.3121 |
45.4283 |
163.3701 |
216.0936 |
-18.98845 |
|
| 76023F |
43060.207900 |
.013845130 |
25.3482 |
10.9980 |
215.4257 |
226.6138 |
-7.22838 |
* |
| 76023J |
09/10/1976 |
.014202330 |
25.2918 |
10.6278 |
215.9062 |
226.5970 |
-7.25248 |
|
| 77092A |
43680.632778 |
.003366272 |
0.1407 |
77.3145 |
256.1496 |
98.8366 |
0.04767 |
-0.13279 |
| |
21/06/1978 |
.000195225 |
0.1356 |
74.7306 |
-50.7829 |
98.5127 |
-0.08512 |
|
| 78113D |
50744.547145 |
.028235910 |
14.1715 |
38.2444 |
177.1164 |
163.1494 |
-22.90318 |
-0.55491 |
| |
23/10/1997 |
.027324530 |
14.1604 |
38.1593 |
166.2476 |
163.8886 |
-23.45809 |
|
| 79087A |
45121.755000 |
.000987337 |
1.6575 |
90.9652 |
196.5378 |
52.5730 |
0.07580 |
-0.08803 |
| |
01/06/1982 |
.000451044 |
1.6578 |
92.3283 |
83.5444 |
52.5333 |
-0.01223 |
|
| 82019B |
45960.349103 |
.000517985 |
0.3705 |
143.1092 |
301.5961 |
201.9020 |
3.06907 |
0.47435 |
| |
17/09/1984 |
.001376090 |
0.3440 |
138.3305 |
35.1682 |
201.7803 |
3.54342 |
|
* Orbital elements of GS 76023F and its fragment 76023J.
Table 2 gives for 9 GS and 5 fragments the magnitude and direction of vector ΔV due to the explosions in orbital system of coordinates longitude l, latitude φ , arguments u0 , distances r0 from the Earth' center and differences r - r0 in km.
Table 2. The change of velocities and directions of motion of objects as a result of explosion and the difference of distances Δr at this moment, calculated from the data of Table 1
| NN |
T (MJD) |
ΔV (m/s) |
l |
φ |
u0 |
r0 (RE) |
Δr (km) |
| 66053J |
47071.689 |
18.27 |
96.°56 |
-1.°16 |
177.°43 |
6.36488 |
2.0 |
| 67066G |
49397.408 |
10.56 |
76.49 |
-5.50 |
271.40 |
6.26042 |
-2.5 |
| 68081E |
48673.398 |
2.70 |
257.35 |
4.92 |
109.21 |
6.51187 |
-6.8 |
| 73040B |
44671.201 |
10.28 |
273.54 |
1.98 |
319.84 |
6.62452 |
-1.5 |
| 73100D |
48718.887 |
3.77 |
80.27 |
7.74 |
326.37 |
7.02865 |
0.2 |
| 77092A |
43680.633 |
9.93 |
272.27 |
-0.29 |
158.40 |
6.61330 |
-1.3 |
| 78113D |
50744.547 |
16.48 |
84.01 |
1.62 |
354.05 |
7.10098 |
-1.0 |
| 79087A |
45121.755 |
4.06 |
273.81 |
21.97 |
123.20 |
6.60815 |
3.9 |
| 82019B |
45960.349 |
4.79 |
248.83 |
39.31 |
180.88 |
6.57548 |
2.7 |
| Fragments |
| 68081G |
48673.398 |
6.60 |
314.07 |
-21.52 |
109.21 |
6.51187 |
7.9 |
| 68081H |
48673.398 |
21.93 |
96.58 |
-6.93 |
109.21 |
6.51187 |
-15.4* |
| 76023J |
43060.208 |
3.89 |
354.55 |
89.01 |
309.98 |
6.70681 |
0.6 |
| 77092H |
43680.633 |
11.38 |
275.84 |
-14.12 |
158.40 |
6.61330 |
-5.2 |
| 79087C |
45121.755 |
10.47 |
101.35 |
2.04 |
123.20 |
6.60815 |
0.3 |
*The fragment 68081H has maximum of discrepancy in Δr. The variation of the rate of drift is in the limits from -0.0015 to -0.0024°/day and the lack of orbital data during 1800 days after explosion is the main reason for these residuals.
MODEL CALCULATION OF FRAGMENT ORBIT EVOLUTION AFTER EXPLOSION
For the investigation of fragment's dynamics after the explosion it is necessary to construct the manifold of fragment orbits assuming a spherically symmetric distribution of their velocity increase ΔV.
The realization of such condition can be done in case of fragment ejection with the equal initial rates into 32 different directions situated on apexes and centers of sides of icosahedron. Beyond the model of 300 fragments was used, with random distribution of directions.
For the moment of each explosion the initial fragment orbits are constructed with the conditions that r=r0 and V=V0+ΔV. These orbits are referred to the Laplace planes with inclinations Λ to equator and their evolutions are calculated. For GS 76023F initial orbits are calculated with ΔV = 250 m/s and in Table 3 the initial data of twelve fragments are given only.
Table 3. The initial orbits of fragments created by explosion GS 76023F for ΔV equal to 250 m/s
76023F Transtage Ò = 43060.207900 MJD
| NN |
l |
φ |
ω |
Ω |
i |
e |
ν |
Λ |
dλ/dt
(°/day) |
r
(RE) |
| 0 |
0° |
0° |
210.°637 |
25.°460 |
17.°842 |
.0138 |
94.°557 |
7.°704 |
-7.228 |
6.6994 |
| 1 |
0 |
90 |
248.338 |
4.553 |
20.751 |
.0150 |
67.147 |
7.895 |
-10.896 |
6.7460 |
| 2 |
0 |
27 |
300.652 |
14.116 |
14.095 |
.1554 |
5.477 |
12.777 |
-86.537 |
7.7446 |
| 3 |
72 |
27 |
0.520 |
11.076 |
17.657 |
.0748 |
308.745 |
9.191 |
-33.912 |
7.0208 |
| 4 |
144 |
27 |
118.151 |
8.696 |
21.817 |
.1199 |
193.591 |
5.090 |
55.313 |
5.9251 |
| 5 |
216 |
27 |
156.638 |
8.713 |
21.773 |
.1285 |
155.085 |
5.135 |
53.960 |
5.9251 |
| 6 |
288 |
27 |
247.587 |
11.150 |
17.537 |
.0984 |
61.600 |
9.313 |
-35.931 |
7.0208 |
| 7 |
36 |
-27 |
307.686 |
27.349 |
13.103 |
.1283 |
345.664 |
11.709 |
-71.970 |
7.5410 |
| 8 |
108 |
-27 |
69.562 |
20.469 |
17.655 |
.0717 |
230.960 |
6.654 |
14.749 |
6.4036 |
| 9 |
180 |
-27 |
127.473 |
18.752 |
19.519 |
.1436 |
174.894 |
4.609 |
70.645 |
5.7472 |
| 10 |
252 |
-27 |
181.761 |
20.573 |
17.567 |
.0942 |
118.651 |
6.748 |
12.634 |
6.4036 |
| 11 |
324 |
-27 |
267.025 |
27.520 |
13.026 |
.1385 |
26.150 |
11.795 |
-73.167 |
7.5410 |
| 12 |
0 |
-90 |
223.657 |
30.446 |
15.410 |
.0150 |
67.147 |
7.894 |
-10.896 |
6.7459 |
The orbital evolution of fragment 2 (Table 3) has shown that the maximum inclination of its orbit with respect to the equator in the process of its evolution can be up to 27°. If at the moment of explosion the node of GS 76023F were 180° instead of 25°, the inclination of the orbit would reach 40°. In case of collision with GS the relative velocity would be about 2 km/s.
During the orbital evolution, the inclination of fragments with respect to the equator can reach 30-40°. Such fragments are especially dangerous for satellites because the collision with them can cause further fragmentation (Kessler, 1993), (Jehn and Flury, 1996). Detailed investigation of the GS 68081E explosion (Pensa et al., 1996) shows that for a fragment of 18 - 20 magnitudes the mean value of ΔV is about 70 m/s. Therefore, it is interesting to study the dynamics of fragments for their search as objects of 18 - 20 magnitude.
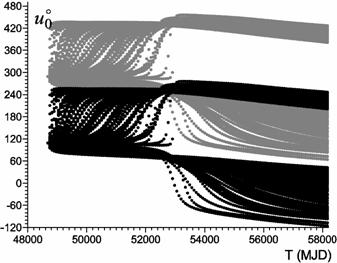
In Figures 2 - 5 the trajectories of intersecting points of GS orbits (with respect to latitude arguments of primary body) by their fragment orbits during about 30 years after the explosion are given (the black lines).
The evolution of the opposite points of intersection (gray lines) is done in a similar way. After several years these points became equivalent because in both points the mutual distances of orbits were reaching many thousands of kilometers.
It has to be noted that most objects during some period have points of intersection consisting of two compact groups at opposite sides of the celestial sphere.
Fig. 2.
The evolution of the intersection points of the orbital plane of GS 68081E with the orbital planes
of its 32 fragments and ΔV = 75 m/s.
Fig. 3.
The evolution of the intersection points of the orbital plane of GS 68081E with the orbital planes
of its 300 fragments and ΔV = 75 m/s.
Fig. 4.
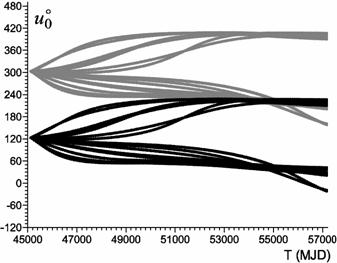
The evolution of the intersection points of the orbital plane of GS 79087A with the orbital planes
of its 32 fragments and ΔV = 75 m/s.
Fig. 5.
The evolution of the intersection points of the orbital plane of GS 79087A with the orbital planes
of its 300 fragments and ΔV = 75 m/s.
In Table 4 the date and equatorial coordinates of such groups are given for several GS. As a rule the length of arc of orbits intersected by fragment during these periods is 20 - 30 . The cases of very long arcs are denoted by asterisks (*).
Table 4. Date and equatorial coordinates of the events of compact intersection GS orbits by fragment orbits.
| Object |
MJD |
Date |
α1 |
δ1 |
α2 |
δ2 |
| 66053J* |
51500 |
1999 |
0h.7 |
+8° |
12h.7 |
-8° |
| 67066G |
51000 |
1998 |
5.6 |
12 |
17.6 |
-12 |
| 68081E |
52800 |
2003 |
3.5 |
11 |
15.5 |
-11 |
| 73040B |
52600 |
2002 |
2.5 |
11 |
14.5 |
-11 |
| 73100D |
57400 |
2016 |
1.0 |
12 |
13.0 |
-12 |
| 77092A |
53500 |
2005 |
3.1 |
11 |
15.1 |
-11 |
| 78113D* |
61000 |
2025 |
3.9 |
9 |
15.9 |
-9 |
| 79087A |
54500 |
2008 |
2.6 |
10 |
14.6 |
-10 |
| 82019B* |
49000 |
1993 |
5.9 |
4 |
19.7 |
-4 |
From Figures 2 - 5 it is clear that for GS 79087A intersection points will exist during MJD 54300-54700, and for GS 68081E - during MJD 52600-53000 (about 26 and 11 years after explosions, respectively).
The search of GS fragments is recommended at the intersection of projection of its orbit on the celestial sphere (Figures 2 - 5). The investigation of such orbits shows that in the intersecting points the mutual distances between orbits periodically became zero, which is the condition for collision. As it is shown in Kiladze et al. (1997) and Sochilina et al. (1999), many uncontrolled satellites collided repeatedly and among them there are also the exploded objects.
CONCLUSIONS
For elaborating effective methods for the safety of controlled satellites in GEO the first step is to study the real situation in this region of a number of exploded objects. It has been shown, that fragments can be found 11-26 years after satellite explosion.
ACKNOWLEDGMENTS
This work was partly supported by INTAS-01-0669.
REFERENCES
- Jehn, R., Collision Risk with Fragments from On-Orbit Breakups, Space Safety and Rescue. AAS Science and Technology Series, 96, pp. 225-239, 1997.
- Jehn, R., and W. Flury, IUE Post-Mission Orbit Options, MAS Technical Note, No 5, ESOC, Darmstadt, 1996.
- Kessler, D.J., Orbital debris environment, Proc. First European Conference on Space Debris, ESA SD-01, Darmstadt, Germany, pp. 251 - 262, 1993.
- Kiladze, R.I., A.S. Sochilina, K.V. Grigoriev, A.N. Vershkov, On investigation of long-term orbital evolution of geostationary satellites, Proc. of 12th Symposium on "Space Flight Dynamics", ESOC, Darmstadt, Germany, 2 - 6 June 1997, pp. 53 - 57, 1997.
- Pensa, A.F., G.E. Powell, E.W. Pork, R. Sridharan, Debris in Geosynchronous Orbits, Space Forum, 1, No 1 - 4, pp. 23 - 37, 1996.
- Sochilina, A.S., R.I. Kiladze, K.V. Grigoriev, A.N. Vershkov, On Occasional Changes of Velocities of Geostationary Satellites, Proceedings of Third US-Russian Space Surveillance Workshop, 20 - 23 October 1998, Editor P.K. Seidelmann, U.S. Naval Observatory, Washington, pp. 339-351, 1999.
- Vershkov A.N., K.V. Grigoriev, R.I. Kiladze, A.S. Sochilina, Model of pollution of the neighborhood of the geostationary orbit by fragments of exploded satellites, Cosmonautics and Rocket Engineering, No 18, pp. 50 - 62, TSNIIMASH, 2000. (In Russian)
E-mail address of A. Sochilina
Manuscript received 11 November 2002; revised 12 March 2003, accepted 30 September 2003
Ðàçìåùåí 6 íîÿáðÿ 2006.
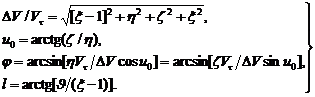 (1)
(1)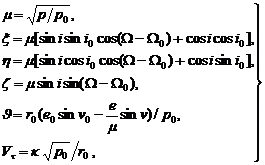 (2)
(2)
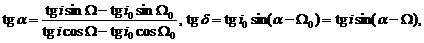 (3)
(3)